3.1. Линии второго порядка. Каноническое уравнение эллипса

Определение. Эллипсом называется геометрическое место точек плоскости для которых сумма расстояний до двух фиксированных точек и , называемых фокусами, есть величина постоянная.

Выведем уравнение эллипса в соответствии с данным определением. Для этого зафиксируем декартову систему координат ХОу как показано на рисунке.

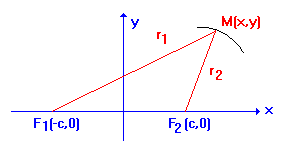
Согласно определению эллипса для точки М имеем , где А - некоторая постоянная. В координатах

.

Подставим эти значения в основное равенство, получим уравнение

.

После стандартного метода "уничтожения" радикалов (возведения обеих частей уравнения в квадрат (см. пример 1.)) получим каноническое уравнение эллипса

(1)

Где . Величины А и B, называются соответственно Большой и Малой Полуосями эллипса.

Замечание. В частности, при из (1) имеем уравнение окружности радиуса А с центром в начале координат

. (2)

Свойства эллипса:

1. Эллипс имеет две взаимно перпендикулярные оси симметрии Х и У (их называют главными осями эллипса) и центр симметрии О (его называют центром эллипса).

Утверждение следует из того, что замена координат на или или не изменяет вид уравнения (1). При этом, в первом случае, при преобразовании , имеем ось симметрии У, во втором - ось симметрии , а в третьем - центр симметрии О.

2. Эллипс полностью содержится в прямоугольнике

.

Из уравнения (1) имеем . Аналогично, .

3. Эллипс получается равномерным сжатием окружности.

Рассмотрим окружность . Произведем равно-мерное сжатие плоскости к оси Ох: . Подставим эти значения в уравнение окружности (2), имеем . После деления на получим уравнение (1).

Построим эллипс на основании его свойств и уравнения (1)

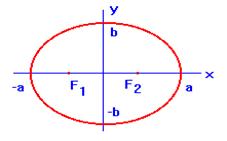
Пример 1. Написать уравнение кривой по которой движется точка M, если сумма расстояний от нее до точек и остается постоянной и равной .

Решение. Согласно условию задачи

.

Откуда

.

Возведем обе части уравнения в квадрат и приведем подобные члены, получим

Еще раз возводим в квадрат и приведем подобные члены

Пример 2. На эллипсе найти точку, расстояние от которой до фокуса в четыре раза больше расстояния чем до фокуса .

Решение. Запишем уравнение эллипса в каноническом виде:

.

Найдем координаты фокусов эллипса

.

Согласно условию задачи

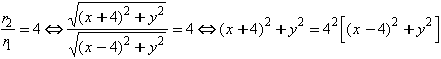Выразим Из уравнения эллипса 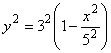, подставим в данное уравнение и приведем подобные члены, получим квадратное уравнение Его корни - лишний корень, т. к. . Тогда 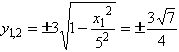. Отв.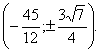

< Предыдущая		Следующая >