2.9.2. Уравнение прямой с угловым коэффициентом

Перепишем каноническое уравнение прямой (2) в виде

, (4)

Где - называется Угловым коэффициентом Прямой , - постоянная.

Построим прямую , заданную уравнением (4).

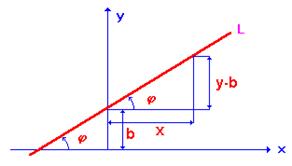
Как видно из построения, B есть величина отрезка, отсекаемого прямой на оси , а есть тангенс угла наклона прямой к оси .

Найдем угол между скрещивающимися прямыми и , заданными угловыми коэффициентами и .

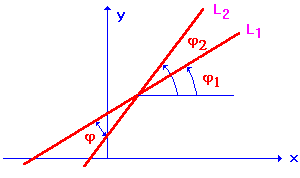
Как видно из рисунка, угол между прямыми и равен . Тогда

. (5)

Замечание. Если поменять местами в (5) и , получим смежный по отношению к угол , такой, что .

Прямые и параллельны, когда , т. е. и как следует из (5) условие параллельности прямых имеет вид . Условие перпендикулярности прямых и соответствует случаю , т. е. знаменатель в (5) равен нулю: . Откуда условие перпендикулярности прямых имеет вид .

Пример 1. Написать уравнение диаметра окружности

,

Перпендикулярного прямой .

Решение. Найдем координаты центра окружности, для чего выделим полный квадрат в уравнении окружности:

.

Найдем угловой коэффициент прямой

По условию ортогональности прямых Искомое уравнение есть уравнение прямой с угловым коэффициентом и проходящей через точку :

Пример 2. Составить уравнение окружности, которая имея центр на прямой , касается прямых , .

Решение. Заметим, что заданные прямые параллельны, следовательно, диаметр окружности равен расстоянию между прямыми. Выберем точку на прямой , например, Тогда,

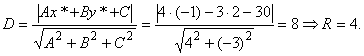
Найдем точки пересечения прямой с прямыми , .

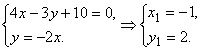
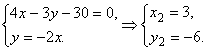
Искомый центр окуружности находится по середине отрезка

Уравнение окружности имеет вид

.

< Предыдущая		Следующая >