2.8.1. Прямая и плоскость в пространстве. Угол между прямой и плоскостью
Пусть заданы плоскость ![]() c нормальным вектором
c нормальным вектором ![]() и прямая
и прямая ![]() с направляющим вектором
с направляющим вектором ![]() ; тогда имеем уравнения
; тогда имеем уравнения
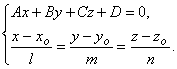 (1)
(1)
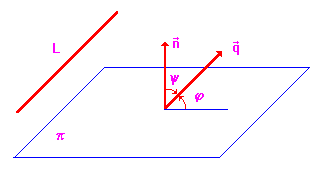
Построим рисунок. Искомый угол ![]() является дополнительным к углу
является дополнительным к углу ![]() . Тогда
. Тогда ![]()
![]() . Откуда
. Откуда
![]() .
.
Условие параллельности прямой ![]() и плоскости
и плоскости ![]() эквивалентно условию
эквивалентно условию ![]() или
или ![]() , т. е.
, т. е. ![]() . Условие перпендикулярности эквивалентно
. Условие перпендикулярности эквивалентно ![]() , т. е.
, т. е.
![]()
Пример 1. Найти угол между прямой ![]() и плос-костью, проходящей через точки
и плос-костью, проходящей через точки
![]() .
.
Решение. Найдем направляющий вектор прямой:

И нормальный вектор плоскости из уравнения плоскости, проходящей через три заданные точки ![]() ,
, ![]()
![]() , не лежащие на одной прямой,
, не лежащие на одной прямой,
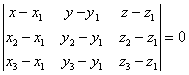 :
:
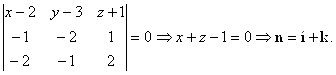
Искомый угол
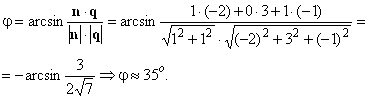
![]()
| < Предыдущая | Следующая > |
|---|