2.3.2. Уравнение плоскости, проходящей через три заданные точки

Очевидно, что три различные фиксированные точки , не лежащие на одной прямой, однозначно определяют некоторую плоскость.

Пусть точка произвольная точка плоскости. Тогда векторы

Компланарные

Смешанное произведение компланарных векторов равно нулю, т. е.

.

В координатах это условие запишется в виде

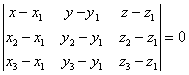(2)

Данное уравнение является искомым уравнением плоскости.

< Предыдущая		Следующая >