1.3. Параметрическое представление плоской линии

Координаты и точек линии можно выразить как непрерывные функции вспомогательной переменной (параметра) , т. е.

.

Это есть параметрическое представление кривой .

В самом деле, из первого равенства выразим и подставим его во второе равенство, получим уравнение (1)

.

Примеры:

7. есть уравнение окружности радиуса R с центром в начале координат.

В самом деле,

.

8. есть уравнение циклоиды.

Определение. Циклоидой называется траектория, которую описывает произвольная точка окружности радиуса , катящаяся по оси, например, .

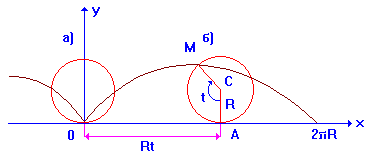
Для вывода уравнения циклоиды зафиксируем начальное положение а) и произвольное положение б), катящейся окружности, и обозначим ее центр С, а точку касания с осью через . Если принять угол поворота радиуса окружности из положения а) с точкой касания до положения б), то

Отсюда следует искомое уравнение.

< Предыдущая		Следующая >