1.2. Линии в полярной системе координат

Переходя в уравнении (1) к полярным координатам имеем , т. е. уравнение линии в полярных координатах

. (2)

Примеры:

5. есть уравнение окружности радиуса с центром в начале координат. В самом деле, подставим в уравнение формулы перехода к полярным координатам , получим

.

6. Использование полярных координат в отдельных случаях эффективнее чем декартовы координаты. Так спираль Архимеда имеет простое уравнение в полярных координатах (Рис.)

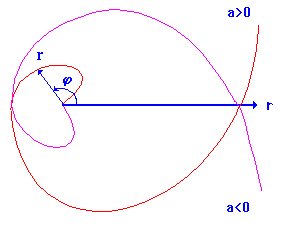
В декартовых координатах эта же кривая описывается систе-мой уравнений

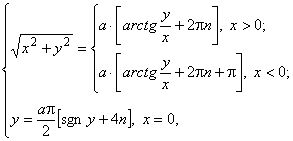
Где .

< Предыдущая		Следующая >