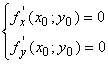8.8. Исследование функций многих переменных на экстремум

Исследование функций многих переменных на экстремум – процедура гораздо более сложная, чем аналогичная процедура для функций одной переменной. Поэтому ограничимся рассмотрением этого вопроса на наиболее простом и наглядном примере функции двух переменных (рис. 8.4). Здесь M1(X1; Y1), M2(X2; Y2), M3(X3; Y3) – точки экстремума этой функции. А именно, точки М1 и М3 – Точки минимума функции, а точка М2 – точка ее максимума. На рис. 8.4 представлена функция с тремя точками экстремума, но этих точек, естественно, может быть и больше, и меньше.

Пусть M0(X0; Y0) – точка какого-либо экстремума (точка максимума или точка минимума) функции . Тогда справедлива

Теорема 1.

Если в точке экстремума M0(X0; Y0) существуют частные производные и , то обе они равны нулю:

(3.1)

Доказательство.

1) Рассмотрим функцию . Так как – экстремальное значение этой функции, то производная этой функции при Х = х0, если она существует, равна нулю:

(3.2)

2) Рассмотрим теперь функцию . Так как – экстремальное значение этой функции, то производная этой функции при Y = Y0, если она существует, равна нулю:

(3.3)

Теорема доказана.

Заметим, что условия (3.1) являются Лишь необходимыми условиями экстремума в точке M0(X0; Y0) дифференцируемой в этой точке функции . То есть эти условия не являются достаточными условиями того, что в точке M0(X0; Y0) функция будет иметь экстремум (максимум или минимум). Иначе говоря, точка M0(X0; Y0), в которой выполняются оба равенства (3.1), является Лишь подозрительной на экстремум точкой для функции . Окончательный вывод о характере такой подозрительной на экстремум точки можно сделать с помощью следующей теоремы (приведем ее без вывода):

Достаточные условия экстремума. Теорема 2.

Пусть M0(X0; Y0) – такая точка из области D Определения функции , что для нее выполняются необходимые условия (3.1) экстремума этой функции. То есть M0(X0; Y0) – подозрительная на экстремум точка. Найдем в этой точке числа

(3.4)

Тогда:

1) Если >0 и >0, то M0(X0; Y0) – точка минимума функции .

2) Если >0 и <0, то M0(X0; Y0) – точка максимума функции .

3) Если <0, то точка M0(X0; Y0) – не точка экстремума функции .

4) Если =0, то вопрос остается открытым – нужно дополнительное исследование.

Пример 1. Пусть Х и У – количества двух произведенных товаров; P1 = 8 руб. и P2 = 10 руб. – цена единицы каждого из этих товаров соответственно; C = 0,01(X2+ Xy+ Y2) – функция затрат (в рублях) на производство этих товаров. Тогда доход R от продажи товаров составит R = 8X+10Y (руб.), а прибыль П составит (в рублях)

П = R – C = 8X + 10Y – 0,01(X2+Xy+Y2).

Найдем объемы Х и У товаров, при которых прибыль П будет максимальной.

1) Сначала найдем значения (Х;у), подозрительные на экстремум для функции П:

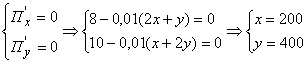
2) Теперь исследуем найденную подозрительную на экстремум для функции П точку М0(200; 400). Для этого найдем в этой точке значения , определяемые выражениями (3.4). Так как

И это верно для любых (Х; у), а значит, и в точке М0(200; 400), то

Так как а то точка М0(200; 400) – точка максимума функции П. То есть прибыль П от продаж будет максимальной при Х = 200 (ед) И У = 400 (ед).

Пример 2. Найти точки экстремума и экстремальные значения функции

Решение. Данная функция – функция двух переменных, определенная для любых Х и У, то есть на всей плоскости Хоу, и имеющая в каждой ее точке частные производные первого порядка:

Сначала найдем точки плоскости Хоу, подозрительные на экстремум для данной функции :

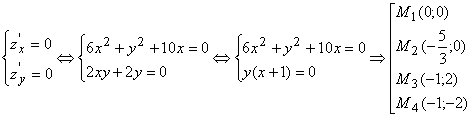
Затем, найдя частные производные второго порядка от функции , запишем выражения для :

Вычисляя теперь числовые значения этих величин для каждой из четырех подозрительных на экстремум точек, получим следующие выводы об этих точках:

- точка max.

- не точка экстремума.

Теперь найдем два экстремальных (максимальных) значения функции , определяющие высоту двух вершин графика этой функции:

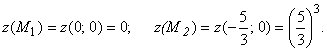
< Предыдущая		Следующая >