8.9. Определение наибольшего и наименьшего значений функциидвух переменных в замкнутой области
Рассмотрим следующую задачу. Пусть ![]() – некоторая непрерывная функция двух переменных, рассматриваемая в замкнутой области
– некоторая непрерывная функция двух переменных, рассматриваемая в замкнутой области ![]() , где
, где ![]() – внутренняя часть области
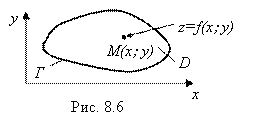
– внутренняя часть области ![]() , а Г – ее граница (рис. 8.6).
, а Г – ее граница (рис. 8.6).
 То, что функция
То, что функция ![]() непрерывна в области
непрерывна в области ![]() , означает, что график этой функции (поверхность в пространстве) является сплошной (без разрывов) поверхностью для всех
, означает, что график этой функции (поверхность в пространстве) является сплошной (без разрывов) поверхностью для всех ![]() . То есть понятие непрерывности функции двух переменных аналогично понятию непрерывности функции одной переменной (см. главу 3, §2). Как и функции одной переменной, функции двух переменных, образованные из элементарных функций, непрерывны для всех значений своих аргументов, для которых они определены. Это касается и функций трех, четырех и более переменных.
. То есть понятие непрерывности функции двух переменных аналогично понятию непрерывности функции одной переменной (см. главу 3, §2). Как и функции одной переменной, функции двух переменных, образованные из элементарных функций, непрерывны для всех значений своих аргументов, для которых они определены. Это касается и функций трех, четырех и более переменных.
Вернемся к рис. 8.6. Поставим следующий вопрос: в каких точках области ![]() функция
функция ![]() достигает своих наибольшего и наименьшего значений ZНаиб И ZНаим? И каковы эти значения? Заметим, что эта задача аналогична той, что была рассмотрена в §3 главы 4 для функции одной переменной
достигает своих наибольшего и наименьшего значений ZНаиб И ZНаим? И каковы эти значения? Заметим, что эта задача аналогична той, что была рассмотрена в §3 главы 4 для функции одной переменной ![]() , рассматриваемой на замкнутом отрезке [A; B] оси Ох.
, рассматриваемой на замкнутом отрезке [A; B] оси Ох.
Очевидно, что искомые точки области ![]() , в которых функция
, в которых функция ![]() достигает своих наибольшего и наименьшего значений, содержатся либо среди точек экстремума этой функции, находящихся внутри области
достигает своих наибольшего и наименьшего значений, содержатся либо среди точек экстремума этой функции, находящихся внутри области ![]() (в области
(в области ![]() ), либо находятся где-то на границе Г этой области. В замкнутой области
), либо находятся где-то на границе Г этой области. В замкнутой области ![]() такие точки заведомо найдутся (теорема Вейерштрасса). А в открытой области
такие точки заведомо найдутся (теорема Вейерштрасса). А в открытой области ![]() (без границы Г) таких точек может и не быть.
(без границы Г) таких точек может и не быть.
Из сказанного выше вытекает следующая Схема нахождения этих точек, аналогичная той, что была изложена в §3 главы 4 для функций одной переменной.
1. Находим все подозрительные на экстремум точки функции ![]() , находящиеся в области D. Это – те точки, в которых обе частные производные
, находящиеся в области D. Это – те точки, в которых обе частные производные ![]() и
и ![]() равны нулю (или одна равна нулю, а другая не существует; или обе не существуют).
равны нулю (или одна равна нулю, а другая не существует; или обе не существуют).
2. Находим все подозрительные на экстремум точки функции ![]() , находящиеся на границе Г области
, находящиеся на границе Г области ![]() . При этом используем уравнение границы Г.
. При этом используем уравнение границы Г.
3. Не исследуя найденные в пунктах 1 и 2 подозрительные точки (это излишне), находим значения функции ![]() во всех найденных подозрительных точках и выбираем те из них, где Z Будет наибольшим и наименьшим.
во всех найденных подозрительных точках и выбираем те из них, где Z Будет наибольшим и наименьшим.
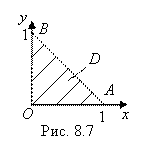 Пример 3. Найти ZНаиб И ZНаим функции
Пример 3. Найти ZНаиб И ZНаим функции ![]() , рассматриваемой в замкнутой области
, рассматриваемой в замкнутой области ![]() , представляющей собой треугольную пластинку с вершинами O(0; 0), A(1; 0), B(0; 1) (рис. 8.7).
, представляющей собой треугольную пластинку с вершинами O(0; 0), A(1; 0), B(0; 1) (рис. 8.7).
Решение. Выполним изложенную выше схему.
1. Найдем внутри треугольника (в области D) точки, подозрительные на экстремум для нашей функции Z. Для этого сначала найдем частные производные первого порядка ![]() и
и ![]() :
:
![]()
Эти производные существуют (их можно вычислить) для любых (х; у). Следовательно, точками, подозрительными на экстремум, будут лишь те, для которых обе эти частные производные равны нулю:
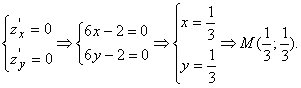
Точка ![]() , очевидно, принадлежит области D (рассматриваемому треугольнику). То есть она – подозрительная на экстремум точка для заданной функции Z внутри треугольника, причем она там единственная.
, очевидно, принадлежит области D (рассматриваемому треугольнику). То есть она – подозрительная на экстремум точка для заданной функции Z внутри треугольника, причем она там единственная.
2. Найдем теперь точки, подозрительные на экстремум, на границе треугольника.
А) Исследуем сначала участок ОА границы (У = 0; 0 £ Х £ 1). На этом участке ![]() – функция одной переменной х. Ее производная
– функция одной переменной х. Ее производная ![]() существует для всех X Î [0; 1]. Поэтому свои экстремальные значения функция Z Может иметь или в точке, где
существует для всех X Î [0; 1]. Поэтому свои экстремальные значения функция Z Может иметь или в точке, где ![]() , то есть в точке
, то есть в точке ![]() , или на концах отрезка ОА, то есть в точках О(0; 0) и А(1; 0).
, или на концах отрезка ОА, то есть в точках О(0; 0) и А(1; 0).
Б) Исследуем теперь участок ОВ границы треугольника (там Х = 0; 0 £ У £ 1). На этом участке функция ![]() (0 £ У £ 1) – функция одной переменной У. Повторяя рассуждения пункта (а), приходим к выводу, что свои экстремальные значения функция Z Может иметь или в точке
(0 £ У £ 1) – функция одной переменной У. Повторяя рассуждения пункта (а), приходим к выводу, что свои экстремальные значения функция Z Может иметь или в точке ![]() , или на концах отрезка ОВ, то есть в точках О(0; 0) и B(0; 1).
, или на концах отрезка ОВ, то есть в точках О(0; 0) и B(0; 1).
В) Наконец, исследуем участок АВ границы. Так как на AB (убедитесь в этом) У = - х + 1 (0 £ Х £ 1), то там функция Z принимает вид: ![]() (0 £ Х £ 1). Ее производная
(0 £ Х £ 1). Ее производная ![]() , поэтому своих экстремальных значений функция Z Может достигать лишь в точке, где
, поэтому своих экстремальных значений функция Z Может достигать лишь в точке, где ![]() , то есть в точке
, то есть в точке ![]() , либо на концах отрезка АВ, то есть в точках А и В.
, либо на концах отрезка АВ, то есть в точках А и В.
Итак, полный набор подозрительных на экстремум точек функции
![]() в треугольнике ОАВ Таков:
в треугольнике ОАВ Таков:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
3. А теперь найдем значения функции Z во всех найденных подозрительных точках и выберем из этих значений наибольшее значение ZНаиб и наименьшее значение ZНаим:
![]()
Таким образом, ZНаиб = 3 и достигается функцией Z В треугольнике ОАВ сразу в двух точках – в его вершинах А и В. А ![]() и достигается функцией Z В треугольнике ОАВ в его внутренней точке
и достигается функцией Z В треугольнике ОАВ в его внутренней точке ![]() .
.
Пример 4. Городской бюджет имеет возможность потратить на социальное жилье не более 600 млн. рублей, располагая при этом проектами и участками земли под 10 пятиэтажных домов на 90 квартир каждый и под 8 девятиэтажных домов на 120 квартир каждый. Средняя сметная стоимость одной квартиры в пятиэтажном доме составляет 400 тысяч рублей, а в девятиэтажном 500 тысяч рублей. Сколько пятиэтажных и сколько девятиэтажных домов должен построить город, чтобы получить максимальное число квартир?
Решение. Пусть Х – искомое количество пятиэтажных домов, У – Девятиэтажных, а Z – Общее количество квартир в этих домах:
Z = 90X + 120Y
Стоимость всех квартир в пятиэтажных домах составит 90 × 0,4·Х = 36Х млн. рублей, а в девятиэтажных 120 × 0,5·У = 60У Млн. рублей. Согласно условиям задачи имеем:
0 £ Х £10; 0 £ У £ 8; 36Х + 60У £ 600
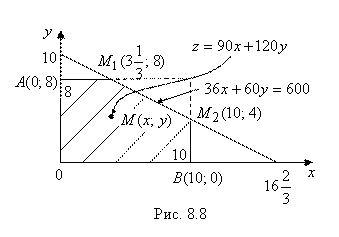 Данные ограничительные неравенства выполняются, очевидно, в пятиугольнике
Данные ограничительные неравенства выполняются, очевидно, в пятиугольнике ![]() (рис. 8.8). В этой замкнутой области
(рис. 8.8). В этой замкнутой области ![]() нужно найти точку М(х; у), для которой функция Z = 90X + 120Y примет наибольшее значение ZНаиб.
нужно найти точку М(х; у), для которой функция Z = 90X + 120Y примет наибольшее значение ZНаиб.
Реализуем изложенную выше схему решения такого рода задач.
1. Найдем внутри пятиугольника точки, подозрительные на экстремум для функции Z. Так как ![]() , и эти частные производные заведомо не равны нулю, то подозрительных на экстремум точек внутри пятиугольника нет.
, и эти частные производные заведомо не равны нулю, то подозрительных на экстремум точек внутри пятиугольника нет.
2. Найдем точки, подозрительные на экстремум, на границах пятиугольника. На каждом из пяти отрезков, составляющих границу пятиугольника, функция Z – линейная функция вида Z = Ax + By, а следовательно, своих наибольшего и наименьшего значений она достигает на границах отрезков. То есть искомое наибольшее значение ZНаиб функция Z достигает в одной из угловых точек (О; А; М1; М2; В). Вычисляя значение Z В этих точках, получим:
Z(О) = 0; z(A) = 960; z(M1) = 1260; z(M2) = 1380; z(B) = 900.
Таким образом ZНаимб = 1380 и достигается оно в точке M2(10; 4). То есть наибольшее число квартир (1380) получится, если будут построены 10 пятиэтажных домов и 4 девятиэтажных.
Упражнения
1. Найти точки экстремума функций:
A) z = 2X + 3Y – x2 – xy – y2; Б) z = x2 – y2; В) z = x4+y4.
Ответ:
А)![]() - точка max; б) нет точек экстремума; в) M0(0; 0) – точка min.
- точка max; б) нет точек экстремума; в) M0(0; 0) – точка min.
2. Найти ZНаиб И ZНаим функции Z = X2 – 2Xy + 3, рассматриваемой в замкнутой области, ограниченной параболой Y = 4 – X2 и осью Ох.
Ответ:
![]() и достигается в точке
и достигается в точке ![]() .
.
![]() и достигается в точке
и достигается в точке ![]() .
.
4. Городской бюджет имеет возможность потратить на социальное жилье не более 600 млн. рублей, располагая при этом проектами и участками земли под 8 пятиэтажных домов на 90 квартир каждый и под 5 девятиэтажных домов на 120 квартир каждый. Средняя сметная стоимость одной квартиры в пятиэтажном доме составляет 600 тысяч рублей, а в девятиэтажном 800 тысяч рублей. Сколько пятиэтажных и сколько девятиэтажных домов должен построить город, чтобы получить максимальное число квартир?
Ответ: 7 пятиэтажных и 2 девятиэтажных.
5. Транспортное предприятия имеет возможность приобрести не более 12 трехтонных и не более 10 пятитонных автомобилей. Цена трехтонного автомобиля составляет 120 тыс. рублей, пятитонного 180 тыс. рублей. Сколько нужно приобрести автомобилей, чтобы их суммарная грузоподъемность была максимальной, если для приобретения автомобилей выделено 2 млн. 400 тыс. рублей.
Ответ: 5 трехтонных и 10 пятитонных.
| < Предыдущая | Следующая > |
|---|