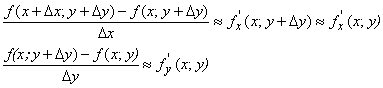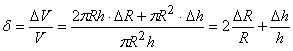8.7. Полный дифференциал функции многих переменных

Для начала рассмотрим это понятие на примере функции двух переменных

. Для этого рассмотрим приращение функции при условии, что аргументы Х и У получат некоторые приращения и :

(2.9)

Если и Малы, то согласно (2.3)

(2.10)

Приближенные равенства (2.10) будут тем точнее, чем меньше и . При этом выражение (2.9) для примет вид:

(2.11)

А теперь будем считать И не просто малыми, а Бесконечно малыми. В этом случае обозначим их символами Dx И Dy соответственно и будем называть Дифференциалами аргументов х и у:

– это бесконечно малое ; – Это бесконечно малое .

(2.12)

При бесконечно малых приращениях аргументов = и = и приращение функции будет, согласно (2.11), бесконечно малым. Обозначим его символом и будем называть Дифференциалом функции :

– это бесконечно малое

(2.13)

При = ; = И = приближенное равенство (2.11) станет уже Точным:

(2.14)

Или короче:

(2.15)

Выражения (2.14) и (2.15) представляют собой так называемый Полный дифференциал функции в точке .

Аналогично, если – функция трех переменных, то ее полный дифференциал в точке найдется по формуле:

(2.16)

Или короче:

(2.17)

А конечное приращение такой функции, соответствующее конечным приращениям , и ее аргументов, найдется по приближенной формуле (2.18), аналогичной формуле (2.11):

(2.18)

Эта формула тем точнее, чем меньше , и .

Полные дифференциалы функций многих переменных являются аналогами полного дифференциала функции одной переменной , который, согласно формуле (5.7) главы 4, определяется равенством:

(2.19)

Полные дифференциалы функций многих переменных – это абстрактные понятия. Они, как и дифференциал функции одной переменной, имеют в основном теоретическое значение. А вот приближенные формулы (2.11), (2.18) и им подобные, определяющие конечное приращение функции при конечных приращениях ее аргументов, широко применяются и на практике.

Пример 4. При измерении размеров цилиндра (его радиуса основания и его высоты ) из-за несовершенства измерительных приборов возможно допущение малых ошибок и соответственно. Найти максимально возможные абсолютную и относительную ошибки при вычислении объема цилиндра.

Решение. Объем цилиндра – функция двух переменных и . Поэтому, используя формулу (2.11), получим следующее приближенное выражение для Абсолютной ошибки при вычислении объема цилиндра :

(2.19)

Ошибки и могут быть любых знаков. При разных знаках этих ошибок ошибка объема цилиндра может быть весьма незначительной. Максимально возможной она будет в том случае, если и будут одинаковых знаков (скажем, обе со знаком (+)). При этом максимально возможная Относительная ошибка при вычислении объема V найдется по формуле:

(2.21)

Упражнения

1. Найти частные производные первого порядка функции

Ответ: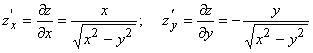

2. Найти частные производные функции первого и второго порядков.

Ответ:

3. Найти приближенное приращение функции в точке М(1; 2) при = 0,1 и = - 0,2. Сравнить полученное приближенное значение с его точным значением.

Ответ:

– приближенно.

– точно.

4. При измерении на местности треугольника получены следующие данные: сторона А = 100М ± 2М; сторона B = 200М ± 3М; угол между ними A = 60° ± 1°. С какой степенью точности (с какой максимальной погрешностью) будет вычислена сторона С ?

Ответ: максимальная погрешность для С составит ±4,35м.

< Предыдущая		Следующая >