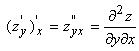8.6. Частые производные и полный дифференциал функций многих переменных
Пусть ![]() – некоторая функция двух переменных. Если зафиксировать одну из переменных (например, У), то функция
– некоторая функция двух переменных. Если зафиксировать одну из переменных (например, У), то функция ![]() Станет функцией лишь одной переменной Х. Если теперь найти производную функции Z по этой оставшейся переменной Х, то эта производная, имеющая несколько разных по форме обозначений
Станет функцией лишь одной переменной Х. Если теперь найти производную функции Z по этой оставшейся переменной Х, то эта производная, имеющая несколько разных по форме обозначений
|
|
(2.1) |
Называется Частной производной функции Z по переменной х. Аналогично определяется, при фиксированном Х И переменном У, Частная производная функции Z = F(X; Y) по переменной Y:
|
|
(2.2) |
Пример 1. Пусть ![]() . Тогда
. Тогда
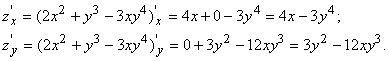
Пользуясь определением производной функции одной переменной (см. главу 4, формулу (1.6)), можем записать и математические определения частных производных функции Z = F(X; Y):
|
|
(2.3) |
Если ![]() – функция трех переменных, то от нее можно вычислить уже три частные производные – по каждой переменной:
– функция трех переменных, то от нее можно вычислить уже три частные производные – по каждой переменной:
|
|
(2.4) |
![]()
Пример 2. Если ![]() то
то

Совершенно аналогично определяются частные производные функций любого числа переменных.
Все это – так называемые частные производные Первого порядка. А если от них снова вычислить (взять) частные производные, то получим уже частные производные второго, третьего и т. д. порядков. Например, если ![]() – функция двух переменных, то
– функция двух переменных, то
|
|
(2.5) |
– частная производная второго порядка от Z По Х;
|
|
(2.6) |
– частная производная второго порядка от Z По Y;
|
|
(2.7) |
– смешанные частные производные второго порядка от Z по Х и У. Кстати, доказано, что если ![]() обе существуют, то они и равны:
обе существуют, то они и равны:
|
|
(2.8) |
То есть результат вычисления смешанных производных не зависит от порядка дифференцирования (если это дифференцирование возможно и в том, и в другом порядка).
Пример 3. Пусть ![]() . Тогда
. Тогда

Примечание. В обозначениях (2.1) – (2.7) для частных производных значок ![]() – с кривым хвостом! В этом его отличие от прямого значка D, применяемого в обозначения (1.4), (2.10), (2.11) для обычных производных функций одной переменной.
– с кривым хвостом! В этом его отличие от прямого значка D, применяемого в обозначения (1.4), (2.10), (2.11) для обычных производных функций одной переменной.
| < Предыдущая | Следующая > |
|---|
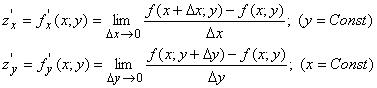
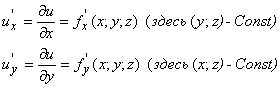
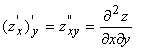 и
и