8.3. Основные понятия, связанные с функциями двух переменных
Пусть Z = F(X; Y) – произвольная функция двух переменных: Х И у – независимые переменные, Z – Функция от этих переменных. Суть такой функции аналогична сути функции одной переменной: (Х; у) ® Z (по Х и У находится Z). Множество D всех тех пар значений независимых переменных (X; Y), для которых можно найти зависимую переменную (функцию) Z, называется областью определения функции Z = F(X; Y). Так как каждая пара чисел (X; Y) представляет собой некоторую точку плоскости Хоу, то область определения D функции Z = F(X; Y) состоит из точек этой плоскости. Если функция Z = F(X; Y)Определена для любых (X; Y), то область D будет занимать всю плоскость Хоу. А если не для любых - то какую-либо ее часть. И для каждой точки M(X; Y) области D можно 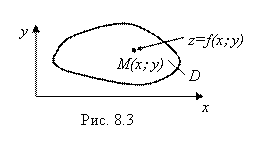 Найти значение величины Z = F(X; Y) (рис. 8.3).
Найти значение величины Z = F(X; Y) (рис. 8.3).
Для наглядности рисунку 8.3 можно придать и какой-нибудь реальный наглядный смысл. Например, можем считать, что D – неравномерно нагретая пластинка, а Z = F(X; Y) – температура в точках M(X; Y) этой пластинки. Или на пластинку D что-то давит, а Z = F(X; Y) – давление на точки M(X; Y) этой пластинки. Или даже D – поле, чем-нибудь засеянное, а Z = F(X; Y) – урожайность посеянной культуры в точках этого поля. И так далее.
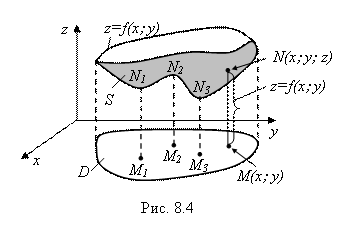 Характер изменения функции Z = F(X; Y) При изменении ее аргументов Х и У (то есть при изменении точки M(х; Y)) можно наглядно изобразить на графике функции. График функции Z = F(X; Y) Состоит из точек N(X; Y; Z) пространства, для которых абсцисса Х и ордината У – это координаты точек M(X; Y) её области определения D, А аппликата находится по формуле Z = F(X; Y) (рис. 8.4).
Характер изменения функции Z = F(X; Y) При изменении ее аргументов Х и У (то есть при изменении точки M(х; Y)) можно наглядно изобразить на графике функции. График функции Z = F(X; Y) Состоит из точек N(X; Y; Z) пространства, для которых абсцисса Х и ордината У – это координаты точек M(X; Y) её области определения D, А аппликата находится по формуле Z = F(X; Y) (рис. 8.4).
То есть графиком произвольной функции Z = F(X; Y) В принципе является некоторая поверхность S в пространстве. Эта поверхность может иметь вершины и впадины (N1; N2; N3; …). Их проекции (M1; M2; M3; …) на плоскость Хоу (на область определения D) называются Точками экстремума функции (точками ее максимума и минимума). Сравнивая рис. 8.2 и 8.4, легко видеть и то общее, что имеется между точками экстремума функций одной и двух переменных, и в чем разница между ними. Есть и математическая схема нахождения точек экстремума функции Z = F(X; Y) (через так называемые частные производные этой функции). Но об этом – позже, в §3.
| < Предыдущая | Следующая > |
|---|