8.2. Основные понятия, связанные с функциями одной переменной

Пусть Y = F(X) – произвольная функция одной переменной: Х – независимая переменная (аргумент), У – функция. Как всем известно, суть этой функции такова: Х ® у (по Х находится У). Множество D Всех тех значений независимой переменной Х, для которых можно найти У, называется областью определения функции Y = F(X). Если функцию Y можно найти для любого Х (-¥ < X < +¥), то есть для любой точки Х числовой оси Ох, то область D Определения этой функции занимает всю ось Ох. Если же это возможно не для любого Х, то область определения D Функции Y = F(X) представляет собой некоторую часть оси Ох – например, отрезок [A; B] (рис. 8.1).

Иллюстрации, изображенной на рис. 8.1, можно для наглядности придать и какой-то реально осязаемый смысл. Например, можно себе представить, что отрезок [A; B] оси Ох – это тонкий материальный стержень, неравномерно нагретый вдоль своей оси, а Y = F(X) – температура в точке Х этого отрезка. Впрочем, функции Y =F(X) можно придать совершенно другой смысл. Например, можно считать, что Y – объем произведенной продукции при затратах Х на ее производство.

Характер изменения функции У при изменении ее аргумента Х очень наглядно демонстрируем график функции, который в принципе представляет собой некоторую линию L на плоскости Хоу (рис. 8.2).

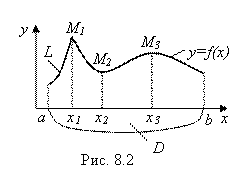
График функции Y = F(X) (линия L) состоит из точек плоскости, координаты (X; Y) которых удовлетворяют уравнению Y = F(X). Точки (M1; M2; M3) – вершины и впадины графика функции, а их проекции на ось оХ (на область определения D Этой функции) называются, как мы знаем, точками экстремума функции (точками ее максимума и минимума). Известна и схема нахождения этих важнейших для функции Y = F(X) точек через ее производную Y´ = F´(X) (см. главу 4, §3).

 

 

< Предыдущая		Следующая >