6.13. Задача Коши для дифференциальных уравнений второго порядка

В §2 мы рассматривали задачу Коши (2.1) для дифференциальных уравнений первого порядка. Она состояла из дифференциального уравнения и начального условия. Начальное условие было предназначено для определения неопределенной константы С, содержащейся в общем решении дифференциального уравнения первого порядка.

Но в общем решении любого дифференциального уравнения второго порядка таких неопределенных констант две (см.(4.4)). Поэтому для их определения нужны два дополнительных (начальных) условия. В качестве таких условий для некоторого начального значения задают начальное значение искомой функции и начальное значение ее производной . В итоге получается задача Коши для дифференциального уравнения второго порядка:

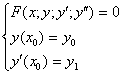(4.21)

Как правило, такая задача имеет единственное решение . Факт существования и единственности решения задачи Коши (4.21) для практических задач вытекает обычно из самого существа рассматриваемой задачи.

Пример 2. Решить задачу Коши:

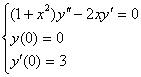(4.22)

Решение. Сначала решим дифференциальное уравнение .

Оно решено выше (см. пример 1); его общее решение, содержащее все его решения, имеет вид

(4.23)

2. Используем начальные условия задачи (4.22) и найдем значения констант и , входящих в (4.23):

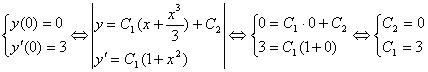(4.24)

3. Подставим =3 и =0 в общее решение (4.23) и получим искомое решение задачи Коши (4.22) (единственное):

(4.25)

< Предыдущая		Следующая >