6.11. Уравнения, не содержащие функции
Это – уравнения вида:
![]() (в уравнении нет
(в уравнении нет ![]() ). (4.4)
). (4.4)
Если ввести новую неизвестную функцию ![]() , зависящую от
, зависящую от ![]() , по формуле
, по формуле
![]()
![]() (4.5)
(4.5)
И учесть, что
![]() , (4.6)
, (4.6)
То уравнение второго порядка (4.4) преобразуется в уравнение первого порядка
![]() (4.7)
(4.7)
Интегрируя его (если это удастся), найдем его общее решение ![]() , а значит, согласно (4.5), получим:
, а значит, согласно (4.5), получим:
![]() (4.8)
(4.8)
Интегрируя теперь уже уравнение (4.8), получим:
![]() (4.9)
(4.9)
Это и есть общее решение уравнения (4.4).
Заметим, что если у уравнения (4.7) окажутся особые решения ![]()
![]() , то будут особые решения
, то будут особые решения
![]()
![]() … (4.10)
… (4.10)
И у уравнения (4.4). Причем, в силу произвольности констант ![]() …, их будет бесчисленное количество.
…, их будет бесчисленное количество.
Пример 1. Решить уравнение
![]() (4.11)
(4.11)
Решение. Данное уравнение является уравнением вида (4.4), так как в нем нет ![]() . Вводя, в соответствии с (4.5) и (4.6), новую неизвестную функцию
. Вводя, в соответствии с (4.5) и (4.6), новую неизвестную функцию ![]() , получим для этой функции уравнение первого порядка:
, получим для этой функции уравнение первого порядка:
![]() (4.12)
(4.12)
Это – дифференциальное уравнение вида ![]() при
при ![]() и при
и при ![]() . То есть, в соответствии с (3.3), это дифференциальное уравнение первого порядка с разделяющимися переменными. Решим его по соответствующей схеме, изложенной в предыдущем параграфе.
. То есть, в соответствии с (3.3), это дифференциальное уравнение первого порядка с разделяющимися переменными. Решим его по соответствующей схеме, изложенной в предыдущем параграфе.
1) ![]() (4.13)
(4.13)
Итак, одно частное решение уравнения (4.12) уже найдено: это функция ![]() .
.
2) Найдем общее решение уравнения (4.12), содержащее все его остальные частные решения:
![]() | разделяем переменные Х и Р |
| разделяем переменные Х и Р |![]()
![]() | интегрируем обе части |
| интегрируем обе части |![]() (4.14)
(4.14)
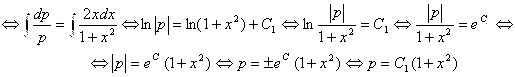
Это – общее решение уравнения (4.12). В него входит и найденное ранее частное решение ![]() (оно получается из общего решения
(оно получается из общего решения ![]() при
при ![]() =0). То есть в него входят все частные решения уравнения (4.12). А теперь, учитывая, что
=0). То есть в него входят все частные решения уравнения (4.12). А теперь, учитывая, что ![]() , получим:
, получим:
![]() (4.15)
(4.15)
Это – общее решение уравнения (4.11). В него входят все частные решения этого уравнения.
| < Предыдущая | Следующая > |
|---|