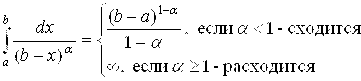5.21. Несобственные интегралы с конечными пределами интегрирования от неограниченных функций
Под указанными несобственными интегралами понимаются интегралы вида 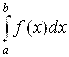 , где F(X) – разрывная в некоторой точке (точках) конечного промежутка интегрирования [A; B] функция, обращающаяся в этих точках в бесконечность (любого знака).
, где F(X) – разрывная в некоторой точке (точках) конечного промежутка интегрирования [A; B] функция, обращающаяся в этих точках в бесконечность (любого знака).
Будем пока считать, что такая точка одна, и эта точка – правая крайняя точка промежутка интегрирования (верхний предел B Интеграла 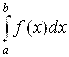 ). То есть будем считать, что функция F(X) непрерывна на полуинтервале [A; B), причем
). То есть будем считать, что функция F(X) непрерывна на полуинтервале [A; B), причем
|
F(x) ® ±¥ при Х ® B |
(6.14) |
Под интегралом 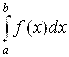 в этом случае, по определению, понимается предел обычного определенного интеграла
в этом случае, по определению, понимается предел обычного определенного интеграла 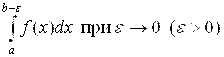 :
:
|
|
(6.15) |
Этот интеграл 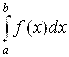 называется Несобственным интегралом от функции, неограниченной на правом конце промежутка интегрирования. Если он существует и конечен, то он называется Сходящимся. Если же не существует или равен +¥ или -¥, то он называется Расходящимся.
называется Несобственным интегралом от функции, неограниченной на правом конце промежутка интегрирования. Если он существует и конечен, то он называется Сходящимся. Если же не существует или равен +¥ или -¥, то он называется Расходящимся.
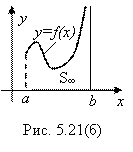
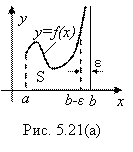
В частности, если F(X)≥0 на [A; B) и F(X) ® +¥ При Х ® B, то геометрическую иллюстрацию равенства (6.15) дают рисунки 5.21(а) и 5.21(б):
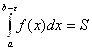
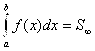 (6.16)
(6.16)
Таким образом, согласно рис. 5.21(б), 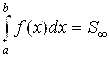 - площадь бесконечно протяженной вдоль оси Оу криволинейной трапеции. А она, как и площадь S¥ На рис. 5.15, может оказаться как конечной, так и бесконечной. То есть несобственный интеграл
- площадь бесконечно протяженной вдоль оси Оу криволинейной трапеции. А она, как и площадь S¥ На рис. 5.15, может оказаться как конечной, так и бесконечной. То есть несобственный интеграл 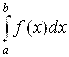 может оказаться как сходящимся, так и расходящимся.
может оказаться как сходящимся, так и расходящимся.
Установить сходимость или расходимость несобственного интеграла 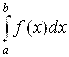 можно на основе его прямого вычисления по формуле Ньютона-Лейбница:
можно на основе его прямого вычисления по формуле Ньютона-Лейбница:
|
|
(6.17) |
Подтвердим это, исходя из определения (6.15):
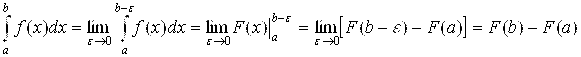
Пример 10. Вычислить несобственный интеграл 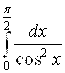 .
.
Решение. Этот интеграл действительно несобственный, так как его подинтегральная функция ![]()
![]() имеет особую точку
имеет особую точку ![]() , в которой
, в которой ![]() , а значит, в которой функция
, а значит, в которой функция ![]() обращается в бесконечность:
обращается в бесконечность:
![]()
Вычисляя указанный интеграл по формуле Ньютона-Лейбница (6.17), получим:
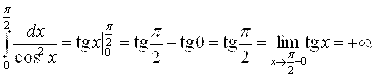
Таким образом, данный несобственный интеграл расходится.
Примечание. Мы ввели понятие несобственного интеграла 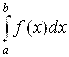 от функции F(X), неограниченной (обращающейся в бесконечность) на правом конце промежутка интегрирования [A; B]. Но этот же интеграл будет несобственным, если F(X) неограничена на левом конце промежутка интегрирования (в точке А), а также в некоторой внутренней его точке С. В последнем случае
от функции F(X), неограниченной (обращающейся в бесконечность) на правом конце промежутка интегрирования [A; B]. Но этот же интеграл будет несобственным, если F(X) неограничена на левом конце промежутка интегрирования (в точке А), а также в некоторой внутренней его точке С. В последнем случае 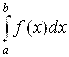 разбивают на два несобственных интеграла:
разбивают на два несобственных интеграла:
|
|
(6.18) |
Оба эти интеграла с особой точкой на краю промежутка интегрирования можно вычислять по формуле Ньютона-Лейбница.
Пример 11. Вычислив несобственный интеграл ![]() , доказать сходимость этого интеграла. Полученному результату дать геометрическую иллюстрацию.
, доказать сходимость этого интеграла. Полученному результату дать геометрическую иллюстрацию.
Решение. Данный интеграл действительно несобственный, так как его подинтегральная функция  обращается в ¥ в точке Х = 0 (
обращается в ¥ в точке Х = 0 (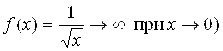 . Вычислим его по формуле Ньютона-Лейбница:
. Вычислим его по формуле Ньютона-Лейбница:

Таким образом ![]() сходится. Его геометрическая иллюстрация дана на рис. 5.22.
сходится. Его геометрическая иллюстрация дана на рис. 5.22.
 Заметим, что вопрос о сходимости-расходимости несобственных интегралов от неограниченных функций, как и вопрос о сходимости-расходимости несобственных интегралов с бесконечными пределами интегрирования, совсем не обязательно выяснять, вычисляя эти интегралы. Можно попробовать сравнить данный несобственный интеграл с каким-либо другим с теми же пределами интегрирования.
Заметим, что вопрос о сходимости-расходимости несобственных интегралов от неограниченных функций, как и вопрос о сходимости-расходимости несобственных интегралов с бесконечными пределами интегрирования, совсем не обязательно выяснять, вычисляя эти интегралы. Можно попробовать сравнить данный несобственный интеграл с каким-либо другим с теми же пределами интегрирования.
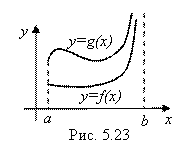 Пусть, например, Y = F(X) и Y = G(X) – две непрерывные в полуинтервале
Пусть, например, Y = F(X) и Y = G(X) – две непрерывные в полуинтервале
[A; B) и неотрицательные функции. И пусть F(X) £ G(X) для всех Х Î [A; B). Пусть, кроме того, F(X) ® +¥ и G(X) ® +¥ При Х ® B (рис. 5.23). Тогда, очевидно,
|
|
(6.19) |
Из этого неравенства очевидным образом вытекает следующий Признак сравнения:
|
А) Если Б) Если |
(6.20) |
В качестве функции G(X), с которой сравнивают данную функцию F(X), часто используют функцию 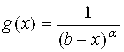 , учитывая при этом, что
, учитывая при этом, что
|
|
(6.21) |
Пример 12. Исследовать на сходимость-расходимость 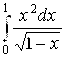 .
.
Решение. Подинтегральная функция  , поэтому данный интеграл является несобственным. При этом очевидно, что для всех Х Î [0; 1)
, поэтому данный интеграл является несобственным. При этом очевидно, что для всех Х Î [0; 1)

Но 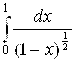 , согласно (6.21), сходится. Поэтому и меньший интеграл
, согласно (6.21), сходится. Поэтому и меньший интеграл 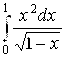 сходится. Более того, можем оценить и значение этого интеграла:
сходится. Более того, можем оценить и значение этого интеграла:
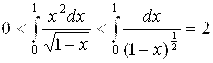 .
.
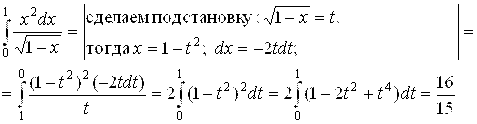
Впрочем, мы можем вычислить этот интеграл и точно:
|
Упражнения
1. Прямым вычислением несобственного интеграла 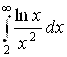 исследовать его на сходимость-расходимость.
исследовать его на сходимость-расходимость.
Ответ:  – интеграл сходится.
– интеграл сходится.
2. Используя признак сравнения (6.7) и учитывая, что 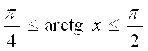 для всех Х Î [1; ¥), исследовать на сходимость интегралы:
для всех Х Î [1; ¥), исследовать на сходимость интегралы:
А) 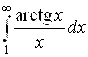 ; б)
; б) 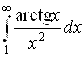 .
.
Ответ: а) сходится; б) расходится.
3. Используя обобщенный признак сравнения (6.9), показать, что из двух несобственных интегралов
А)  ; б)
; б) 
Интеграл (а) расходится, а интеграл (б) сходится.
4. Показать, что 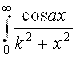 при А ¹ 0 и K ¹ 0 сходится абсолютно.
при А ¹ 0 и K ¹ 0 сходится абсолютно.
5. Показать, что 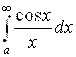 при любом А > 0 сходится условно.
при любом А > 0 сходится условно.
6. Вычислив несобственный интеграл 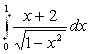 , подтвердить его сходимость.
, подтвердить его сходимость.
7. Вычислив несобственный интеграл 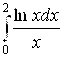 , подтвердить его расходимость.
, подтвердить его расходимость.
8. Используя признак сравнения (6.20), показать, что несобственный интеграл 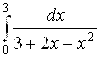 расходится. Подтвердить это прямым вычислением интеграла.
расходится. Подтвердить это прямым вычислением интеграла.
| < Предыдущая | Следующая > |
|---|
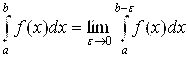

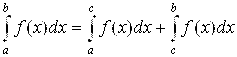
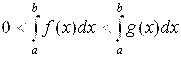
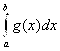 = (число)– сходится, то и
= (число)– сходится, то и 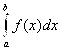 =(число)– сходится.
=(число)– сходится. – расходится, то и
– расходится, то и 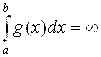 – расходится
– расходится