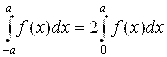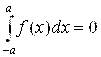5.19. Использование четности-нечетности подинтегральной функции при вычислении определенных интегралов с симметричными пределами интегрирования

А) Если F(X) – непрерывная и четная на промежутке [-A; а] функция, то

(5.9)

Б) Если F(X) – непрерывная и нечетная на промежутке [-A; A] функция, то

(5.10)

Доказательство. Рассмотрим рисунки 5.13 (а) и 5.13 (б), соответствующие случаям (а) и (б) соответственно.

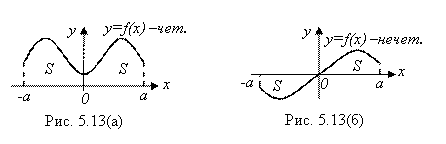
а) Если F(X) – четная на [-A; A] функция, то согласно рис. 5.13 (а) и формулы (4.3) получаем:

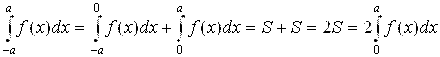
Б) Если F(X) – нечетная на [A; B] функция, то согласно рис. 5.13 (б) и формулам (4.3) и (4.5) получаем:

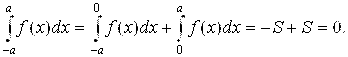
Пример 3. Упростить, а затем и вычислить

Решение.

Упражнения

1. Вычислить с помощью подходящих подстановок:

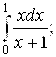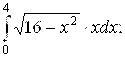А) б) в)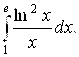

Ответы: А) 1 – Ln2; б) ; в) .

2. Вычислить интегрированием по частям:

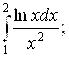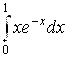А) б) ; в)

Ответы: А) б) в) .

3. Вычислить 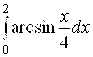, сделав в этом интеграле сначала подстановку , а затем применив интегрирование по частям.

Ответ:

< Предыдущая		Следующая >