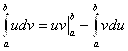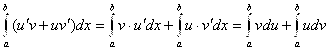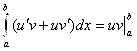5.18. Вычисление определенных интегралов по частям
Мы уже знаем, что по частям можно вычислять неопределенные интегралы. Для этого используется формула (2.2). Но по частям можно вычислять и определенные интегралы. Это делается по внешне похожей формуле (5.5):
|
|
(5.5) |
Здесь ![]() и
и ![]() – Любые две непрерывные на [A; B] функции, имеющие на этом промежутке и непрерывные производные
– Любые две непрерывные на [A; B] функции, имеющие на этом промежутке и непрерывные производные ![]() И
И ![]() (то есть
(то есть ![]() и
и ![]() - непрерывно дифференцируемые на [A; B] функции).
- непрерывно дифференцируемые на [A; B] функции).
Докажем формулу (5.5). Учтем, что
|
|
(5.6) |
Функция ![]() , стоящая в этом равенстве справа, согласно указанных выше условий для функций
, стоящая в этом равенстве справа, согласно указанных выше условий для функций ![]() и
и ![]() , является непрерывной на промежутке [A; B]. Значит, существует определенный интеграл от нее:
, является непрерывной на промежутке [A; B]. Значит, существует определенный интеграл от нее:
|
|
(5.7) |
С другой стороны, согласно (5.6), функция ![]() является первообразной для функции
является первообразной для функции ![]() . А значит, по формуле Ньютона-Лейбница получаем:
. А значит, по формуле Ньютона-Лейбница получаем:
|
|
(5.8) |
Сравнивая (5.7) и (5.8), приходим к доказываемой формуле (5.5).
Пример 2. Вычислить 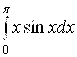 .
.

| < Предыдущая | Следующая > |
|---|