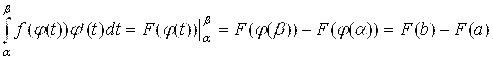5.17. Подстановка в определенных интегралах
Пусть Y = F(X) – непрерывная на промежутке [A; B] оси Ox Функция, а ![]() - непрерывная на промежутке [α; β] функция, имеющая к тому же на [α;β] непрерывную производную (то есть X = φ(T) – непрерывно дифференцируемая на [α; β] функция). Кроме того, будем считать, что когда переменная T меняется от α До β, то переменная X = φ(T) меняется от A до B. Таким образом, φ(α) = B и φ(β) = B. Тогда при вычислении
- непрерывная на промежутке [α; β] функция, имеющая к тому же на [α;β] непрерывную производную (то есть X = φ(T) – непрерывно дифференцируемая на [α; β] функция). Кроме того, будем считать, что когда переменная T меняется от α До β, то переменная X = φ(T) меняется от A до B. Таким образом, φ(α) = B и φ(β) = B. Тогда при вычислении 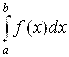 можно совершить подстановку по следующей схеме:
можно совершить подстановку по следующей схеме:
|
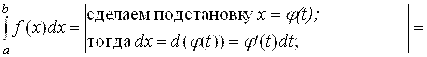
|
 (5.1)
(5.1)
Докажем правомочность схемы (5.1). Пусть
|
|
(5.2) |
Здесь F(X) – некоторая первообразная для функции F(X). То есть F΄(X) = F(X). Но тогда, по правилу вычисления производной сложной функции,
|
|
(5.3) |
Поэтому по формуле Ньютона-Лейбница
|
|
(5.4) |
Равенство результатов (5.2) и (5.4) и доказывает правомочность схемы (5.1).
Кстати, сравнивая схему (5.1) вычисления определенных интегралов с помощью подстановки с аналогичной схемой (2.1) вычисления неопределенных интегралов, можно увидеть и то, что в этих схемах общее, и то, что различно.
Примечание. На практике часто бывает удобнее делать подстановку не вида X = φ(T), а вида T = φ(X).
| < Предыдущая | Следующая > |
|---|