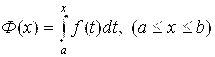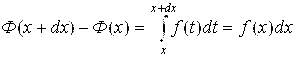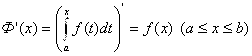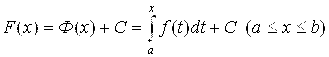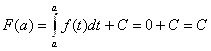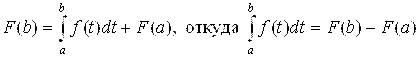5.16. Вычисление определенных интегралов (приближенное и точное). Формула Ньютона-Лейбница

Определенный интеграл 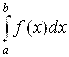, согласно его математическому определению (4.2), представляет собой сумму бесконечно большого числа бесконечно малых слагаемых, образованных по схеме рисунка 5.5. Для непрерывной подынтегральной функции F(X) и конечных пределов интегрирования A и B этот интеграл, как было показано выше, заведомо существует (представляет собой некоторое число). Но найти его напрямую, следуя указанной на рис. 5.5 схеме, очевидно, невозможно. По этой схеме его можно найти лишь приближенно.

Для этого промежуток интегрирования [A; B] следует разбить не на бесконечно малые участки Dx, которых будет бесконечно много, а на конечное число (скажем, на 100) частичных промежутков одинаковой (или не одинаковой) конечной длины . Затем на каждом выбрать некоторую точку Х (скажем, середину) и подсчитать сумму

Из уже конечного числа (из 100) слагаемых. Эта сумма будет Приближенным значением определенного интеграла 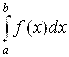. Если нужно получить более точный результат, то нужно сделать более мелкое разбиение промежутка интегрирования (скажем, разбить его не на 100 частичных промежутков, а на 200, 300, и т. д.). Собственно, таким путем (с некоторыми непринципиальными усовершенствованиями указанной схемы) и вычисляют приближенно определенные интегралы на ЭВМ. ЭВМ умеют, кстати, оценивать точность полученного результата, и при вычислении определенных интегралов за счет своего быстродействия способны достигать любой разумной точности (до нескольких тысяч десятичных знаков после запятой). Но вычисляя таким путем определенные интегралы, абсолютно точного результата, тем не менее, ЭВМ дать не в состоянии.

И тут возникает вопрос: а нельзя ли все-таки вычислять определенные интегралы абсолютно точно? Ответ на это вопрос такой: можно, хотя далеко и не всегда. Для точного подсчета определенных интегралов, если оно возможно, применяется знаменитая формула Нютона-Лейбница.

Суть ее в следующем. Пусть F(X) – непрерывная на [A; B] функция, так что 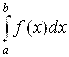заведомо существует. И пусть вычислен неопределенный интеграл от функции F(x):

(4.19)

Тогда Точное значение 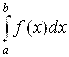можно найти по формуле:

(4.20)

Здесь F(X) – любая первообразная для функции F(X). Формула (4.20) называется Формулой Ньютона-Лейбница.

Для доказательства формулы Ньютона-Лейбница докажем сначала, что функция

(4.21)

То есть определенный интеграл с переменным верхним пределом, имеет на [A; B] производную Ф΄(X), совпадающую с F(X) (Ф΄(X) = F(X)).

Действительно,

(4.22)

Но

(4.23)

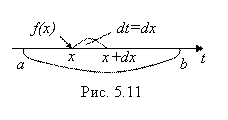В последнем интеграле интегрирование происходит на бесконечно малом промежутке [X; X+Dx] оси T длиной Dx. На нем, при его разбиении на бесконечно малые промежутки Dt, уместится лишь один такой промежуток Dt = Dx
(см. рис. 5.11). Выбирая на нем в качестве произвольно выбираемой точки T точку X и следуя схеме (4.2) вычисления определенного интеграла, получим по этой схеме лишь одно слагаемое:

(4.24)

А значит, согласно (4.22), получаем:

(4.25)

Отметим, что заодно мы доказали следующий принципиальный факт, который мы обещали доказать в конце §2: у любой непрерывной на [A; B] функции F(X) имеется первообразная F(X). Ею, в частности, является функция Ф(х). А значит, для любой непрерывной на [A; B] функции F(X) существует для X Î [A; B] и неопределенный интеграл (4.19). Хотя, как мы уже замечали в §1, он далеко не всегда может быть выражен через элементарные функции (может оказаться неберущимся). Найдя приближенно (машинным путем) функцию Ф(х), мы тем самым найдем приближенно и .

А теперь перейдем непосредственно к доказательству формулы Ньютона-Лейбница (4.20). Пусть F(X) – любая первообразная для функции F(X) на [A; B]. Так как она может отличаться от указанной выше первообразной Ф(х) лишь на константу, то

(4.26)

Полагая в этом равенстве Х = а, получаем:

(4.27)

Значит, равенство (4.26) принимает вид:

(4.28)

А теперь, полагая в (4.28) Х = B, получим:

(4.29)

Но это, по сути, это и есть формула (4.20) Ньютона-Лейбница.

Пример 3. Вычислить .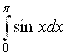

Решение. Вычислим сначала

(значит, )

А тогда

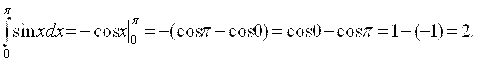
Геометрическая иллюстрация полученного результата изображена ниже:

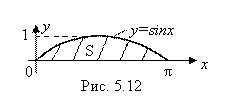
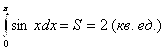(4.30)

Формула Ньютона-Лейбница (4.20) принадлежит к числу важнейших формул высшей математики. Она позволяет просто, а главное, точно вычислять определенные интегралы. А значит, позволяет находить точные значения многих нужных для практики величин (площадей криволинейных фигур; помещений тел при переменных скоростях их движения; работ переменных сил и многое другое). Но она может быть использована, если только соответствующий неопределенный интеграл – из берущихся. В противном случае неизвестна первообразная F(X) для функции F(X), а значит, нечего подставлять и в формулу (4.20) Ньютона-Лейбница.

Если неопределенный интеграл неберущийся, то соответствующий ему определенный интеграл 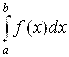может быть найден лишь приближенно. Например, с помощью ЭВМ – так, как об этом говорилось выше, перед выводом формулы Ньютона-Лейбница.

Упражнения

1. На основании формулы (4.18) (формулы грубой оценки определенных интегралов) оценить величину следующих интегралов:

А); б).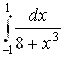

Ответ: а); б).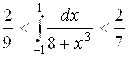

2. Сравнив подынтегральные функции интегралов и 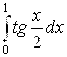, выяснить, какой из них больше.

Ответ: > .

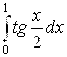3. Доказать, что для всех справедливо неравенство , и с его помощью доказать, что

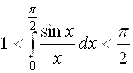
4. Доказать, что 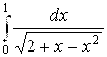заключен между и .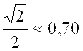

5. Найти площадь S, заключенную между параболой и осью оХ.

Ответ: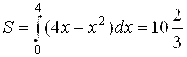

6. Найти работу А, которую нужно затратить, чтобы растянуть пружину на 6 см, если для ее растяжения на 1 см необходима сила в 20 н.

Указание. При решении задачи использовать закон Гука: величина удлинения пружины пропорциональна растягивающей ее силе.

Ответ: .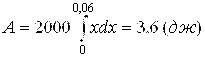

7. Производительность труда Z = F(T) среднестатистического рабочего на некотором предприятии представляет собой функцию

Найти объем Q продукции, производимой рабочим за смену (8 часов).

Ответ: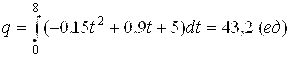

< Предыдущая		Следующая >