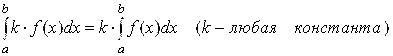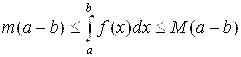5.15. Свойства определенных интегралов
|
1) |
(4.8) |
(число А может быть любого знака).
|
2) |
(4.9) |
(переменную интегрирования в определенном интеграле можно обозначить как угодно – результат не изменится).
|
3) |
(4.10) |
(ибо если перемещение точки отсутствует, то работа любой силы F(X) равна нулю).
|
4) |
(4.11) |
(ибо если сила отсутствует, то и работа отсутствует).
|
5) |
(4.12) |
(ибо работа постоянной единичной силы численно равна перемещению точки под действием этой силы).
|
6) |
(4.13) |
|
|
(4.14) |
|
8) |
|
9) |
(4.16) |
|
10) Если f(x) ≤ g(x) для всех xÎ[a; b], то |
(4.17) |
(физический смысл последних пяти свойств продумать самостоятельно).
11) Пусть M = [F(X)]Наим И М = [F(X)]Наиб – соответственно наименьшее и наибольшее значения функции F(X) на промежутке [A; B]. Тогда
|
|
(4.18) |
Действительно, так как M ≤ F(X)≤ M для всех XÎ [A; B], то применяя свойство (4.17) и затем свойства (4.16) и (4.12), мы и получим двойное неравенство (4.18). Это неравенство часто используется для прикидки (Грубой оценки) величины 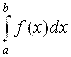 .
.
Пример 1. Оценить величину 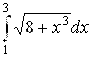 .
.
Решение. Так как функция ![]() монотонно возрастает на отрезке [1; 3], то
монотонно возрастает на отрезке [1; 3], то ![]() Поэтому по формуле грубой оценки (4.18) получаем:
Поэтому по формуле грубой оценки (4.18) получаем:
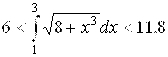
Пример 2. Оценить величину 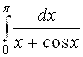 .
.
Решение. Минимальное M и максимальное M значения функции ![]() на промежутке [0; p] не очевидны, так как с возрастанием Х в выражении X + Cos X первое слагаемое растет, а второе убывает. Чтобы разобраться в поведении функции Y, найдем ее производную:
на промежутке [0; p] не очевидны, так как с возрастанием Х в выражении X + Cos X первое слагаемое растет, а второе убывает. Чтобы разобраться в поведении функции Y, найдем ее производную:
 .
.
Так как Sin X ≤ 1 для всех Х, то ![]() для всех Х. А значит, функция
для всех Х. А значит, функция ![]() убывает на всей области своего определения, в том числе и на отрезке [0; p]. Таким образом, на отрезке [0; p]
убывает на всей области своего определения, в том числе и на отрезке [0; p]. Таким образом, на отрезке [0; p]
![]()
Следовательно, оценка (4.18) для данного интеграла имеет вид:
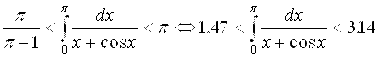
| < Предыдущая | Следующая > |
|---|
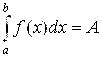 – число
– число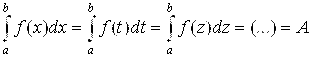
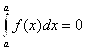
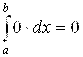
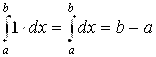
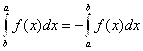
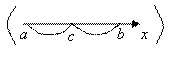 7)
7) 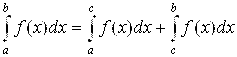
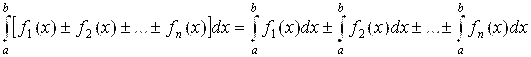 (4.15)
(4.15)