5.14. Основные свойства определенных интегралов
 Наиболее просто и естественно установить эти свойства, опираясь на какой-либо наглядный смысл определенного интеграла. Например, на то, что любой определенный интеграл
Наиболее просто и естественно установить эти свойства, опираясь на какой-либо наглядный смысл определенного интеграла. Например, на то, что любой определенный интеграл 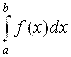 Связан, согласно (4.3), (4.5) и (4.6), с площадями криволинейных трапеций. Но использовать этот геометрический смысл определенного интеграла для вывода его свойств в самом общем случае, то есть в случае знакопеременной функции Y = F(X), не очень удобно. Гораздо удобнее и нагляднее установить эти свойства, если, в соответствии с (3.12), считать определенный интеграл
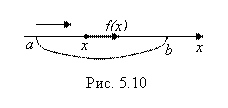
Связан, согласно (4.3), (4.5) и (4.6), с площадями криволинейных трапеций. Но использовать этот геометрический смысл определенного интеграла для вывода его свойств в самом общем случае, то есть в случае знакопеременной функции Y = F(X), не очень удобно. Гораздо удобнее и нагляднее установить эти свойства, если, в соответствии с (3.12), считать определенный интеграл 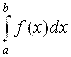 работой А силы F(X) (силы любого направления, а значит, и любого знака), когда точка приложения Х этой силы перемещается вдоль оси Ох из положения А в положение B (рис. 5.10).
работой А силы F(X) (силы любого направления, а значит, и любого знака), когда точка приложения Х этой силы перемещается вдоль оси Ох из положения А в положение B (рис. 5.10).
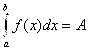 (4.7)
(4.7)
Тогда сразу становятся очевидными следующие
| < Предыдущая | Следующая > |
|---|