5.12. Задача о нахождении объема производства при заданной производительности труда

Пусть функция описывает изменение производительности труда рабочего, бригады или целого предприятия с течением времени . Требуется найти формулу для объема произведенной продукции с момента времени до момента времени , где и - заданные числа.

Решение. Если бы производительность труда (количество продукции, производимой в единицу времени) была постоянной, то искомый объем произведенной продукции мы нашли бы, умножив производительность труда на время работы, то есть нашли бы по формуле. Но, по условию, производительность труда меняется со временем. Чтобы в этом случае найти искомый объем произведенной продукции, нужно, очевидно, разбить промежуток времени на бесконечно малые промежутки времени , выбрать внутри каждого произвольную точку , найти объем произведенной за время продукции, и сложить все - то есть по существу проделать ту же процедуру, что была проделана в предыдущих трех задачах. В итоге получим формулу

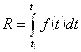, (3.13)

Совершенно аналогичную формулам (3.4), (3.8) и (3.12). Эта формула выражает объем продукции, произведенной за время от до , через производительность труда .

Итак, мы получим итоговые формулы (3.4), (3.8), (3.12) и (3.13) для четырех рассмотренных выше и имеющих важное практическое значение задач. Можно было бы и продолжить рассмотрение аналогичных задач, но мы ограничимся теми, что уже рассмотрели. Вместо этого осмыслим ту общую идею, которая была заложена при решении всех этих задач. А эта идея следующая: нужную нам величину мы мысленно разбиваем на бесконечно малые части, а затем, складывая все эти части (их бесконечно много!), получаем искомую величину. Эта величина оказывалась выраженной через новое математическое понятие - определенный интеграл. Теперь, очевидно, нужно понять, какими свойствами обладают определенные интегралы и как их вычислять.

Упражнения

1. Пусть отрезок [А; B] оси Ox – материальная нить, у которой - заданная линейная плотность вещества, распределенного по этой нити (линейная плотность - это масса единицы длины). Получить формулу для массы всей нити.

Ответ: 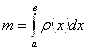(3.14)

2. Пусть – объем тела вращения, образованного вращением криволинейной трапеции (рис. 5.1(а)) вокруг оси Ox . Получить формулу для объема этого тела.

Ответ: 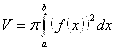(3.15)

3. Пусть – длина участка кривой с абсциссами концов и (рис. 5.1(а)). Получить формулу для длины этого участка.

Ответ: (3.16)

< Предыдущая		Следующая >