5.11. Задача о нахождении работы переменной силы

Пусть по оси Ох из точки A в точку B под действием заданной переменной силы движется материальная точка (точка приложения силы ) - см. рис. 5.3. 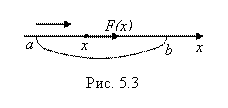Требуется вывести формулу для работы А, которую совершит сила F(X) При перемещении материальной точки Х из положения А в положение B.

Решение. Если бы сила , приложенная к движущейся точке , была постоянной, то мы нашли бы работу по известной школьной формуле . Но у нас сила переменная - она меняется с изменением координаты движущейся точки. В связи с этим разобьем мысленно промежуток [А; B] на бесконечно малые участки длиной и найдем работу силы на каждом участке (рис. 5.4).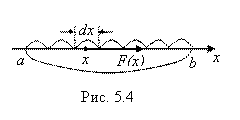

Если – некоторая точка на участке , то очевидно, что

(3.9)

Мы записали эту формулу, считая, что в любой точке, находящейся на данном участке , сила, действующая на движущуюся точку, такая же, как и в выбранной точке , то есть постоянная. Но это, вообще говоря, не так: во время прохода точкой участка действующая на нее сила, хоть и незначительно, но меняется. Впрочем, изменение этой силы на тем меньше, чем меньше . А значит, с уменьшением формула (3.9) будет становиться все точнее и точнее. Но так как наш участок не просто мал, а бесконечно мал, то формулу (3.9) мы вправе считать Точной.

А теперь, складывая работы силы на всех участках , на которые мы разбили отрезок [А; B], мы получим, Причем точно, всю искомую работу А:

(3.10)

А так как, по аналогии с равенствами (3.2) и (3.7),

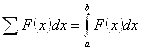, (3.11)

То получим окончательно:

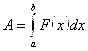(3.12)

Это и есть формула для работы А, которую совершит переменная сила , если её точка приложения переместится вдоль оси Ох из положения в положение (рис. 5.3).

< Предыдущая		Следующая >