5.10. Задача о вычислении пути при переменной скорости движения

Пусть некоторая материальная точка движения по некоторой траектории с известной в каждый момент времени переменной скоростью Требуется получить формулу для пути (перемещения), пройденного точкой по траектории своего движения с некоторого данного момента времени до некоторого данного момента времени .

Решение. Если бы скорость движения точки была постоянной, то поставленная задача никакого труда бы не представляла: путь равен скорости, умноженной на время. То есть . Но у нас скорость точки переменная (в разные моменты времени она разная). Для такого случая разобьем мысленно временной промежуток на бесконечно малые промежутки времени и найдем путь , проходимый точкой за каждое время .

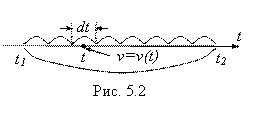
Рассмотрим один из промежутков (любой) и выберем на этом промежутке некоторую точку (некоторый момент времени) . В этот момент времени скорость движения точки равна (рис.5.2). Практически такой же, в силу малости , она будет в других точках (в другие моменты времени) этого же промежутка времени. То есть можем считать, что в течение времени Точка движется практически с постоянной скоростью . А тогда путь , пройденный точкой за время , найдется по формуле:

(3.5)

Впрочем, таким был бы путь , если бы в течение времени Точка двигалась строго с постоянной скоростью . Но эта скорость хоть и незначительно, но все же меняется в течение времени . Поэтому формула (3.5) не точная, а приближенная. Однако очевидно, что с уменьшением времени Она будет становиться все точнее и точнее. А так как наш промежуток времени не просто мал, а Бесконечно мал, то мы вправе считать формулу (3.5) Точной.

Складывая теперь пути , Пройденные точкой за все промежутки времени , найдем, Причем точно, и общий путь (общее перемещение точки по траектории ее движения) за время от момента до момента :

(3.6)

Формула (3.6) по своей структуре совершенно аналогична формуле (3.2). Она, как и формула (3.2), представляет собой сумму бесконечно большого числа бесконечно малых слагаемых. То есть представляет собой определенный интеграл вида (3.3):

(3.7)

Итак, получаем окончательно: если - переменная скорость движения точки, то перемещение , пройденное точкой по траектории ее движения, найдется по формуле:

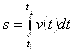(3.8)

< Предыдущая		Следующая >