5.09. Задача о вычислении площади произвольной криволинейной трапеции

 

 

 

 

 

 

 

 

 

 

 

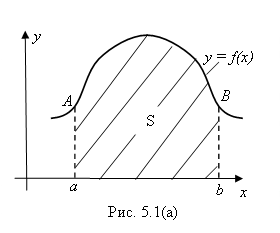
Рассмотрим рис. 5.1(а), где – некоторая непрерывная на функция.

Заштрихованная на этом рисунке фигура называется Криволинейной трапецией. А S - площадь этой трапеции. Поставим, вслед за Ньютоном и Лейбницем, задачу: вывести формулу для площади S этой трапеции при заданных A, B И F(X).

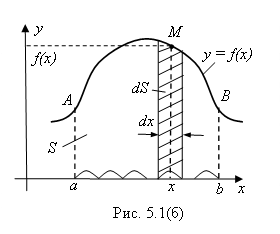
Решение. Разобьем мысленно отрезок оси Ох (основание трапеции) на бесконечно малые участки, как это показано на рис. 5.1(б). Для простоты будем считать их одинаковыми по длине. Эту бесконечно малую длину каждого участка обозначим символом Dx. Если через концы этих участков провести вертикальные прямые, то вся криволинейная трапеция разобьется на бесконечно большое число бесконечно узких вертикальных полосок шириной Dx. Рассмотрим одну из таких полосок (любую), и найдем ее площадь DS (см. рис. 5.1(б)).

Возьмем в основании полоски некоторую произвольную точку Х. Так как полоска бесконечно узкая (то есть она представляет собой вертикальную нить), то Х – это точка, являющаяся основанием этой нити. Согласно рис. 5.1(б), площадь DS Рассматриваемой полоски (нити) можно найти, умножив ее высоту F(X) на ширину Dx. То есть

DS = F(X)Dx (3.1)

Впрочем, такой была бы площадь DS полоски, если бы полоска была прямоугольником с основанием Dx и высотой F(X). Но наша полоска имеет сверху криволинейную границу, а F(X)- Высота, на которой находится лишь одна из точек (точка М) этой границы. Все остальные точки указанной верхней границы полоски находятся, вообще говоря, на другой, хоть и близкой к F(X), Высоте. Так что формула (3.1) для площади каждой из полосок, на которые мы мысленно разбили криволинейную трапецию, не точная, а приближенная. Но очевидно, чем уже полоска, тем точнее формула для ее площади DS. А так как наша полоска (как и все остальные) не просто узкая, а Бесконечно узкая, то мы вправе считать формулу (3.1) Точной.

Складывая теперь площади DS Всех вертикальных полосок, найдем, Причем точно, и всю площадь S криволинейной трапеции:

(3.2)

Эта сумма необычная: слагаемые в ней бесконечно малые, а число слагаемых бесконечно велико (S - сумма бесконечно большого числа бесконечно малых слагаемых). Этой сумме Лейбниц дал специальное обозначение.

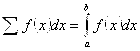(3.3)

И назвал ее Определенным интегралом от функции F(X). Здесь F(X)– подинтегральная функция; F(X)Dx - подиНтегральное выражение; X – переменная интегрирования; A и B - пределы интегрирования (нижний и верхний).

Итак, согласно (3.2) и (3.3),

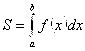(3.4)

- площадь криволинейной трапеции, изображенной на рис. 5.1(а).

< Предыдущая		Следующая >