4.25. Свойства эластичности функции
1. Эластичность функции ![]() равна произведению независимой переменной X на так называемый Темп изменения функции
равна произведению независимой переменной X на так называемый Темп изменения функции 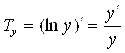 :
:
![]() (7.2)
(7.2)
2. Эластичность произведения двух функций равна сумме эластичностей этих функций:
![]() (7.3)
(7.3)
3. Эластичность частного двух функций равна разности эластичностей этих функций:
 (7.4)
(7.4)
Отметим, что последние два свойства – прямое следствие формулы (7.2) и свойств логарифма:
![]() ;
; ![]()
4. Эластичность взаимно обратных функций – взаимно обратные величины:
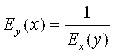 (7.5)
(7.5)
Действительно,

Эластичность экономических функций применяется при анализе этих функций. Выясним, например, как влияет эластичность или неэластичность спроса Q относительно цены P единицы продукции на суммарный доход от продаж ![]() при условии, что зависимость спроса Q на товар от его цены P имеет некоторое уравнение
при условии, что зависимость спроса Q на товар от его цены P имеет некоторое уравнение ![]() . Это уравнение так называемой кривой спроса, которая, очевидно, является убывающей кривой (с увеличением цены P единицы товара спрос Q на этот товар, естественно, уменьшается) – см. рис. 4.6.
. Это уравнение так называемой кривой спроса, которая, очевидно, является убывающей кривой (с увеличением цены P единицы товара спрос Q на этот товар, естественно, уменьшается) – см. рис. 4.6.
Подсчитаем предельный (маржинальный) доход от продаж:
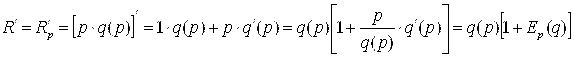 (7.6)
(7.6)
Где
 (7.7)
(7.7)
– эластичность спроса Q относительно цены P. Так как и P, и Q неотрицательны, а ![]() , как производная убывающей функции, отрицательна, то
, как производная убывающей функции, отрицательна, то ![]() .
.
Если спрос эластичен, то есть если ![]() (а значит,
(а значит, ![]() ), то, согласно (7.6),
), то, согласно (7.6), ![]() . А это значит, что зависимость дохода R от цены P является убывающей. То есть с увеличением цены P единицы продукции суммарный доход R от продаж будет уменьшаться. А с уменьшением цены – наоборот увеличиваться. Но уменьшение цены P автоматически ведет к увеличению спроса Q. Таким образом, при эластичном спросе с увеличением спроса Q увеличивается и доход R. То есть При эластичном спросе каждая дополнительно проданная единица продукции приносит дополнительный доход.
. А это значит, что зависимость дохода R от цены P является убывающей. То есть с увеличением цены P единицы продукции суммарный доход R от продаж будет уменьшаться. А с уменьшением цены – наоборот увеличиваться. Но уменьшение цены P автоматически ведет к увеличению спроса Q. Таким образом, при эластичном спросе с увеличением спроса Q увеличивается и доход R. То есть При эластичном спросе каждая дополнительно проданная единица продукции приносит дополнительный доход.
Если спрос неэластичен, то есть если ![]() (а значит,
(а значит, ![]() ), то, согласно (7.6),
), то, согласно (7.6), ![]() . То есть зависимость R от P будет возрастающей. Иначе говоря, с увеличением цены P единицы продукции суммарный доход от продаж R будет увеличиваться. А с уменьшением цены – уменьшаться. Но уменьшение цены автоматически ведет к увеличению спроса, то есть к увеличению объема продаж. И при этом, тем на менее, доход R будет уменьшаться! То есть При неэластичном спросе каждая дополнительно произведенная и проданная единица продукции будет приносить не доход, а убыток.
. То есть зависимость R от P будет возрастающей. Иначе говоря, с увеличением цены P единицы продукции суммарный доход от продаж R будет увеличиваться. А с уменьшением цены – уменьшаться. Но уменьшение цены автоматически ведет к увеличению спроса, то есть к увеличению объема продаж. И при этом, тем на менее, доход R будет уменьшаться! То есть При неэластичном спросе каждая дополнительно произведенная и проданная единица продукции будет приносить не доход, а убыток.
Наконец, если ![]() (
(![]() ), то есть если спрос имеет единичную эластичность, то
), то есть если спрос имеет единичную эластичность, то ![]() . А это значит, что изменением цены P (а значит, и с изменением объема продаж Q) суммарный доход от продаж R не изменится.
. А это значит, что изменением цены P (а значит, и с изменением объема продаж Q) суммарный доход от продаж R не изменится.
Если изобразить зависимости ![]() ,
, ![]() и
и ![]() графически, то результаты проведенного исследования предстанут в виде:
графически, то результаты проведенного исследования предстанут в виде:
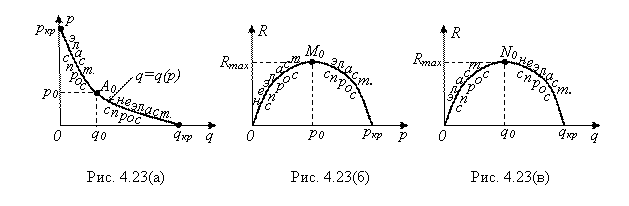
Здесь P0 и Q0 – оптимальная цена и оптимальный спрос (объем продаж), обеспечивающие максимум дохода R. Им соответствует единичная эластичность спроса. То есть оптимальная цена P0 единицы товара может быть найдена из уравнения:
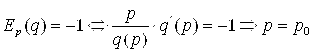 (7.8)
(7.8)
А оптимальный спрос Q0 может быть найден из уравнения кривой спроса: ![]() .
.
Впрочем, если известны явные выражения ![]() и
и ![]() , то значения P0 и Q0 проще найти из равенств:
, то значения P0 и Q0 проще найти из равенств:
![]() ;
; ![]() (7.9)
(7.9)
Согласно рис. 4.23 (б), дохода не будет вообще (![]() ), когда товар ничего не стоит (
), когда товар ничего не стоит (![]() ), или когда цена P достигнет критического значения
), или когда цена P достигнет критического значения![]() , при котором товар перестанут покупать вообще (этой цене соответствует спрос
, при котором товар перестанут покупать вообще (этой цене соответствует спрос ![]() – см. рис. 4.23 (а). А согласно рис. 4.23 (в) доход от продаж товара будет нулевым, если объем продаж Q будет нулевым (этому соответствует критическая цена товара
– см. рис. 4.23 (а). А согласно рис. 4.23 (в) доход от продаж товара будет нулевым, если объем продаж Q будет нулевым (этому соответствует критическая цена товара ![]() ), или если объем продаж Q достигнет некоторого значения
), или если объем продаж Q достигнет некоторого значения ![]() , которому, очевидно, соответствует нулевая цена
, которому, очевидно, соответствует нулевая цена ![]() единицы товара. То есть
единицы товара. То есть ![]() – это тот максимальный объем товара, который покупатели возьмут, если он отдается даром. Имея явные зависимости
– это тот максимальный объем товара, который покупатели возьмут, если он отдается даром. Имея явные зависимости ![]() и
и ![]() , можно найти и
, можно найти и ![]() , и
, и ![]() . Впрочем, естественнее они находятся из уравнения
. Впрочем, естественнее они находятся из уравнения ![]() кривой спроса.
кривой спроса.
Пример 2. Пусть уравнение кривой спроса ![]() – линейная убывающая функция
– линейная убывающая функция ![]() , где
, где ![]() и
и ![]() . При этом и функция
. При этом и функция ![]() – линейная и убывающая. Суммарный доход от продаж
– линейная и убывающая. Суммарный доход от продаж ![]() можно выразить двояко:
можно выразить двояко:
А) ![]() ; б)
; б)  (7.10)
(7.10)
Графики обеих этих функций – параболы, направленные ветвями вниз, то есть они представляют собой кривые типа тех, что изображены на рисунках 4.23 (б) и 4.23 (в).
Оптимальную цену P0 и оптимальный спрос Q0 легко найти по схемам (7.9):
А) ![]() (7.11)
(7.11)
б) ![]()
При этом
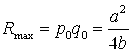 (7.12)
(7.12)
Критические значения ![]() и
и ![]() цены и спроса найдем, приравняв доход R к нулю:
цены и спроса найдем, приравняв доход R к нулю:
А) ![]() (7.13)
(7.13)
б) 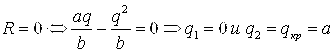
Эластичность ![]() спроса Q относительно цены P тоже можно выразить двояко – и через P, и через Q:
спроса Q относительно цены P тоже можно выразить двояко – и через P, и через Q:
А)  ; (7.14)
; (7.14)
б)  .
.
 На основании формул (7.14) легко убедиться в том, что при оптимальной цене
На основании формул (7.14) легко убедиться в том, что при оптимальной цене ![]() (или, что одно и то же, при оптимальном спросе
(или, что одно и то же, при оптимальном спросе ![]() ) эластичность спроса
) эластичность спроса ![]() , то есть спрос имеет единичную эластичность. При
, то есть спрос имеет единичную эластичность. При ![]() (
(![]() ) эластичность
) эластичность ![]() , то есть спрос будет эластичным. При
, то есть спрос будет эластичным. При ![]() (
(![]() ) имеем
) имеем ![]() , то есть спрос будет неэластичным.
, то есть спрос будет неэластичным.
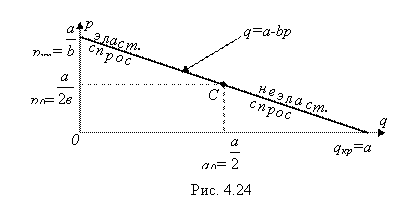
Все установленное выше можно наглядно проиллюстрировать и на кривой спроса ![]() (рис. 4.24).
(рис. 4.24).
Отметим, что значение Q0 объема продаж, обеспечивающее максимум дохода от продаж R, еще не обеспечивает максимума прибыли П от продаж данного товара. Действительно, ![]() , где С – издержки производства (себестоимость товара):
, где С – издержки производства (себестоимость товара):
![]() (7.15)
(7.15)
Прибыль ![]() будет максимальной при том Q, при котором
будет максимальной при том Q, при котором ![]() :
:
![]() (7.16)
(7.16)
Таким образом, прибыль от производства будет максимальной при том объеме продаж Q, при котором предельный доход ![]() равен предельным издержкам
равен предельным издержкам ![]() . А это – известный экономический закон.
. А это – известный экономический закон.
Наконец, рассмотрим прибыль П предприятия, если кроме издержек производства с каждой единицы произведенной продукции берется налог T. Тогда при объеме Q произведенной продукции суммарный налог Т составит ![]() рублей, а общая прибыль предприятия П выразится формулой:
рублей, а общая прибыль предприятия П выразится формулой:
![]() (7.17)
(7.17)
Максимум прибыли при заданном налоге T предприятие будет иметь при том объеме продаж Q, который соответствует уравнению:
![]() (7.18)
(7.18)
При этом суммарный налог Т с проданной продукции составит
![]() (7.19)
(7.19)
Можно поставить вопрос: при каком T, то есть при какой ставке налога, суммарный налог Т будет максимальным? (в этом заинтересованы налоговые органы). Это будет то значение T, при котором ![]() :
:
![]()
Подставляя найденное значение ![]() в выражение (7.18) для
в выражение (7.18) для ![]() , получим:
, получим: ![]() . Это тот объем производства, при котором при максимуме суммарной прибыли П предприятия будет максимальным и суммарный налог Т на продукцию этого предприятия.
. Это тот объем производства, при котором при максимуме суммарной прибыли П предприятия будет максимальным и суммарный налог Т на продукцию этого предприятия.
Пример 3. Пусть
![]() ;
; ![]()
Тогда
![]()
![]()
![]() ;
; ![]()
![]() .
.
Таким образом, максимальная прибыль ![]() составит:
составит:
![]()
А максимальный налог Т составит:
![]()
Интересно сопоставить эти цифры с цифрами при отсутствии налогообложения, то есть при ![]() . В этом случае (убедитесь в этом самостоятельно)
. В этом случае (убедитесь в этом самостоятельно) ![]() ;
; ![]() . Следовательно, уменьшение налогообложения стимулирует выпуск дополнительной продукции и приводит при этом к резкому увеличению прибыли от ее реализации. Отсюда ясно, почему производители прикладывают столько усилий, чтобы снизить ставку налога T.
. Следовательно, уменьшение налогообложения стимулирует выпуск дополнительной продукции и приводит при этом к резкому увеличению прибыли от ее реализации. Отсюда ясно, почему производители прикладывают столько усилий, чтобы снизить ставку налога T.
В экономической теории находят применение не только производные первого порядка, но и производные второго порядка.
Один из знаменитых экономических законов – Закон убывающей доходности – звучит так: с увеличением производства дополнительная продукция, полученная на каждую новую единицу производственного ресурса (например, численности рабочих, капитальных затрат на производство и т. д.) с некоторого значения этого ресурса убывает.
Сформулируем этот закон на языке математики. Пусть ![]() – зависимость объема Y выпускаемой продукции от используемого на ее производство ресурса X. И пусть
– зависимость объема Y выпускаемой продукции от используемого на ее производство ресурса X. И пусть ![]() – дополнительная продукция, полученная при использовании дополнительного к X ресурса
– дополнительная продукция, полученная при использовании дополнительного к X ресурса ![]() . Тогда:
. Тогда:
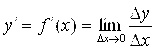 (7.20)
(7.20)
– продукция, полученная на единицу дополнительного (к X) ресурса. Согласно закона убывающей доходности, эта продукция с некоторого ![]() убывает. А это значит, что с некоторого
убывает. А это значит, что с некоторого ![]() производная функции (7.20) отрицательна:
производная функции (7.20) отрицательна:
![]() (при
(при ![]() ) (7.21)
) (7.21)
 Вспоминая геометрический смысл второй производной, приходим к выводу, что при
Вспоминая геометрический смысл второй производной, приходим к выводу, что при ![]() график функции
график функции ![]() является выпуклым (а до того, при
является выпуклым (а до того, при ![]() , он был вогнутым) – рис. 4.25. Данное обстоятельство является отправной точкой для дальнейшего исследования указанной зависимости Y от X. В частности, для подбора аналитического вида
, он был вогнутым) – рис. 4.25. Данное обстоятельство является отправной точкой для дальнейшего исследования указанной зависимости Y от X. В частности, для подбора аналитического вида ![]() этой зависимости.
этой зависимости.
Упражнения
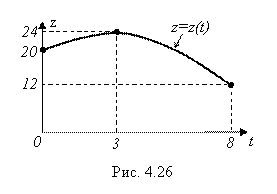
1. Опытным путем установлено, что объем Q продукции, производимой на предприятии в течение рабочей смены, определяется формулой:
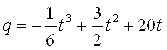 (ед.)
(ед.)
 Здесь
Здесь ![]() – рабочее время в часах. Исследовать зависимость
– рабочее время в часах. Исследовать зависимость ![]() производительности труда на этом предприятии от времени и построить график этой зависимости.
производительности труда на этом предприятии от времени и построить график этой зависимости.
Ответ:
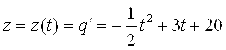 (ед./час)
(ед./час)
2. Опытным путем установлены уравнения кривых спроса и предложения:
 ;
;  .
.
Здесь Q и S – это соответственно количества продаваемого и предлагаемого к продаже товара при цене единицы товара P.
 А) Построить кривые спроса и предложения.
А) Построить кривые спроса и предложения.
Б) Найти равновесную цену P0 единицы товара, при которой спрос равен предложению.
В) Найти эластичность спроса и эластичность предложения относительно цены P при этой равновесной цене и прокомментировать их экономический смысл.
Ответ:
Б) ![]() ; при этом
; при этом ![]() (ед.)
(ед.)
В) 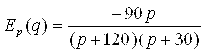 ;
; 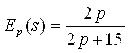 .
.
При равновесной цене ![]() получаем:
получаем:
![]() ;
; ![]()
Это значит, что при увеличении цены P единицы товара на 1 % от равновесной цены ![]() (с 30 до 30,3) спрос на товар Q уменьшится на 0,3 %, а предложение от производителей товара S увеличится на 0,8 %. То есть появится товарный излишек в объеме 1,1 %.
(с 30 до 30,3) спрос на товар Q уменьшится на 0,3 %, а предложение от производителей товара S увеличится на 0,8 %. То есть появится товарный излишек в объеме 1,1 %.
Обратно, если цена P уменьшится на 1 %, то спрос Q увеличится на 0,3 %, а предложение уменьшится на 0,8 %. То есть возникнет товарный дефицит в объеме 1,1 %.
| < Предыдущая | Следующая > |
|---|