4.21. Свойства дифференциала функции

1.

2.

3.

4.

5. 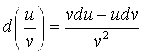(5.11)

Здесь С – любая константа, а , и – любые дифференцируемые функции. Действительно:

1. ;

2. .

Совершенно аналогично доказываются и остальные свойства (5.11).

Пусть теперь и – любые две дифференцируемые функции. Тогда – сложная функция от X. И ее дифференциал Dy, как оказывается, можно найти по любой из двух следующих формул:

1) ; 2) (5.12)

Формулы (5.12) выражают так называемое Свойство инвариантности формы дифференциала функции. Согласно этого свойства, дифференциал функции имеет форму произведения производной этой функции на дифференциал ее аргумента независимо от того, является ли ее аргумент независимой переменной (X) или функцией (U) от другого аргумента.

Действительно, если X – независимая переменная, то дифференциал Dy функции Y, зависящей от X, находится, в соответствии с (5.6), по первой из формул (5.12). Но так как – сложная функция от X, то используя формулу (2.5) для производной сложной функции, получим:

То есть приходим ко второй формуле (5.12).

< Предыдущая		Следующая >