4.22. Дифференциалы высших порядков

Найдя дифференциал Dy данной функции , можем затем найти дифференциал от этого дифференциала. Тем самым получим так называемый Дифференциал второго порядка данной функции :

.

Итак, если – некоторая дважды дифференцируемая функция, то ее дифференциал второго порядка (дэ два игрек) находится по формуле:

(5.13)

Отсюда, кстати, получаем:

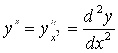, где (5.14)

Тем самым находит свое оправдание обозначение Лейбница (2.10) для производной второго порядка функции . Аналогично получает оправдание и обозначение (2.11) для производной третьего порядка, которая выражается через дифференциал (дэ три игрек) третьего порядка

, откуда 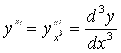, (5.15)

И т. д.

Отметим еще одно существенное обстоятельство. Дифференциал Dy функции Y (дифференциал первого порядка), как показано выше, имеет инвариантную (неизменную) форму независимо от того, является ли аргумент X функции Y независимой переменной или, наоборот, сам является функцией от другой переменной. А вот для дифференциалов высших порядков (, , …) Эта инвариантность места не имеет.

Действительно, пусть – сложная функция от T. Тогда, согласно инвариантности формы первого дифференциала Dy, имеем:

.

А вот

(5.16)

Действительно,

Упражнения

1. Найти дифференциалы первого и второго порядков следующих функций:

А) ; б) ; в) , где U – дифференцируемая функция некоторой независимой переменной.

Ответ:

А) ; .

Б) ; .

В) ; .

2. С помощью приближенной формулы (5.3) найти абсолютную и относительную погрешности вычисления объема куба со стороной X, если при измерении X допущена ошибка .

Ответ: ;

– абсолютная погрешность;

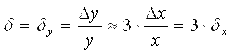– относительная погрешность.

3. Как известно, площадь круга S радиуса R находится по формуле , а объем шара V радиуса R – по формуле . Используя приближенную формулу (5.3), найти:

А) площадь тонкого кругового кольца с внутренним радиусом R и шириной ;

Б) объем тонкой сферической оболочки с внутренним радиусом R и толщиной . Сравнить эти приближенные выражения с точными.

Ответ:

А)

Б)

4. Используя формулу (5.9) для функции , вычислить приближенно .

Ответ: .

5. Кривая спроса имеет линейный вид (; ). Найти изменение спроса на товар при изменении на цены P единицы этого товара.

Ответ: .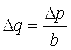

6. Пусть зависимость себестоимости продукции Y от объема произведенной продукции X выражается формулой . Найти изменение себестоимости произведенной продукции, если объем X продукции увеличится с 15 ед. до 15,2 ед.

Ответ: себестоимость вырастет на денежных единицы.

< Предыдущая		Следующая >