4.20. Дифференциал функции

Понятие дифференциала функции тесно связано с понятием ее производной. Как и производная функции, дифференциал функции принадлежит к числу важнейших понятий математического анализа и введен в математику Ньютоном и Лейбницем параллельно с понятием производной.

Вспомним определение производной функции в некоторой фиксированной точке X (§ 1, формулы 1.5 и 1.6):

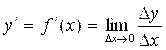(5.1)

Здесь – приращение аргумента X, а – соответствующее приращение функции Y.

Будем считать, что данная функция дифференцируема в рассматриваемой фиксированной точке X. То есть будем считать, что производная в этой точке существует и конечна. Тогда, согласно (5.1),

при (5.2)

А это значит, что при малых значениях будем иметь:

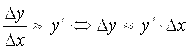(5.3)

Причем приближенные равенства (5.3) будут тем точнее, чем меньше (и соответственно чем меньше ).

А теперь будем считать приращение аргумента функции не просто малым, а Бесконечно малым, и назовем его Дифференциалом аргумента x. Введем (следуя Лейбницу) для него и специальное обозначение:

Dx – дифференциал аргумента X. (5.4)

Таким образом, Дифференциал Dx аргумента X – это бесконечно малое приращение этого аргумента. Конечно, только что введенное понятие дифференциала переменной X – математическая абстракция (она сродни диаметру точки или толщине линии). Но математика постоянно пользуется абстракциями, поэтому еще одна абстракция пугать нас не должна.

Если приращение аргумента X бесконечно мало (), то и приращение функции Y тоже будет бесконечно мало. Обозначим его символом Dy и будем называть Дифференциалом функции Y. Так как , то

– дифференциал функции Y. (5.5)

Если теперь в приближенных равенствах (5.3) заменить малые, но конечные и на бесконечно малые Dx и Dy, то эти равенства станут Точными.

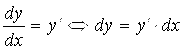(5.6)

Оба равенства (5.6) имеют важный смысл. Первое из них дает выражение производной функции Y через отношение дифференциалов Dy и Dx функции и аргумента. А второе дает выражение дифференциала функции Dy через производную функции и дифференциал аргумента Dx.

Кстати, если учесть, что , то последнее равенство (5.6) можно записать подробнее:

(5.7)

А если еще учесть исходное выражение (5.5) для дифференциала функции , то из последнего равенства получаем:

(5.8)

Равенство (5.8) позволяет записать значение функции в точке , бесконечно близкой к точке X, через значение функции и ее производной в самой точке X. Эта формула имеет большое теоретическое значение.

Если в равенстве (5.8) заменить бесконечно малое Dx на малое, но конечное , то вместо точного оно станет приближенным:

(5.9)

Равенство (5.9) называется Простейшим вариантом формулы Тейлора. Эта приближенная формула тем точнее, чем меньше . Она используется для приближенного вычисления значения по значениям и . У формулы (5.9) имеется и ясный геометрический смысл – мы его укажем в следующем параграфе. Там же мы приведем и полный вариант формулы Тейлора.

В частности, применяя эту формулу для функций ; ; ; , и т. д., получим следующие интересные формулы для производства приближенных вычислений:

1) ; ( – в радианах) 2) 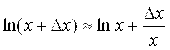; (5.10)

3) ; ;

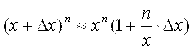4) ; ;

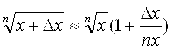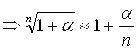В частности, используя последнюю формулу, получим:

.

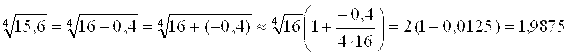Для сравнения: точное значение . То есть приближенное значение , полученное вручную, отличается от его точного значения лишь в четвертом знаке после запятой.

Вернемся все же к формулам (5.6) и (5.7), служащим для нахождения дифференциала функции . На базе этих формул можно установить следующие

< Предыдущая		Следующая >