4.14. Нахождение наибольшего и наименьшего значений функции, . непрерывной на отрезке

Пусть – функция, непрерывная на некотором отрезке оси Ох (рис. 4.13)

Ставится задача: указать схему нахождения тех точек отрезка оси Ох, в которых функция достигает своего наибольшего значения и своего наименьшего значения , и найти эти и .

Сразу отметим, что такие точки на отрезке заведомо существуют (это доказано). А вот на интервале их может и не быть. То есть на интервале функция своих наибольшего и наименьшего значений может и не иметь. Например, функция на отрезке свое наименьшее значение достигает в точке , а свое наибольшее значение достигает в точке . А вот на интервале своих наибольшего и наименьшего значений функция , очевидно, не имеет (не достигает).

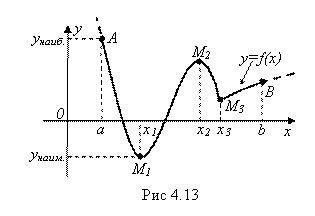
Вернемся к рис. 4.13, на котором изображена произвольная непрерывная на отрезке функция . Здесь достигается функцией на конце A отрезка , а – в точке X1, являющейся одной из точек минимума функции. И вообще, очевидно, что и при любой другой форме графика непрерывной функции наибольшее и наименьшее значения достигаются ею на отрезке или в её точках экстремума, содержащихся на этом отрезке, или на концах отрезка. Отсюда вытекает следующая

Схема нахождения и Функции На отрезке :

1. Находим производную .

2. Находим принадлежащие отрезку точки, подозрительные на экстремум.

3. Не исследуя этих точек, вычисляем значение функции во всех найденных подозрительных точках, а также на концах A и B отрезка . Из всех найденных значений Y выбираем и . А заодно и устанавливаем, в каких точках отрезка эти и достигаются.

Пример 2. На отрезке найти наибольшее и наименьшее значения функции .

Решение. Реализуем изложенную выше схему.

1. Найдем :

.

2. Найдем на отрезке точки (значения X), подозрительные на экстремум:

А) .

Б) не существует Þ таких X нет.

На отрезке содержатся лишь две подозрительные на экстремум точки: это и .

3. Вычисляем значении функции в обеих найденных подозрительных точках, а также на концах отрезка, и выберем из найденных значений функции наибольшее и наименьшее:

; ; ;

Ответ: ; .

< Предыдущая		Следующая >