4.13. Схема исследования функции на возрастание-убывание . и точки экстремума

1. Находим область определения функции. То есть находим все те значения X, для которых существует (можно найти) значение функции . Заодно устанавливаем интервалы непрерывности и точки разрыва функции.

2. Находим производную .

3. Находим точки (значения X), подозрительные на экстремум. То есть находим те точки (значения X), в которых производная функции или равна нулю, или не существует:

а)

б) не существует

4. Наносим все найденные в пунктах (а) и (б) подозрительные на экстремум точки на область определения функции (на ось Ох) и фиксируем (например, дугами) интервалы, на которые разобьется область определения этими точками. Так как внутри каждого такого интервала производная функции существует и не обращается в нуль, то в каждом интервале производная сохраняет свой знак, который может измениться лишь при переходе к другому интервалу. С помощью вычисления производной в пробных внутренних точках определяем знак производной в каждом интервале. По найденным знакам производной устанавливаем интервалы возрастания и убывания функции, а по смене знака производной определяем точки экстремума функции (точки максимума и минимума).

5. В найденных точках максимума и минимума вычисляем значения функции и тем самым определяем вершины и впадины графика функции, отмечая заодно, округлые они или острые.

Пример 1. Исследовать функцию На возрастание-убывание и точки экстремума.

Решение. Действуем по изложенной выше схеме.

1. Функция определена (а следовательно, и непрерывна) для любых X, то есть на всей числовой оси Ох (). Значит, её график – сплошная (без разрывов) линия.

2. Найдем производную :

.

3. Найдем точки (значения X), подозрительные на экстремум:

А) .

Б) не существует Þ таких X нет.

4. Нанесем найденные подозрительные на экстремум точки и на область определения функции (на ось Ох). Ось Ох этими точками разобьется на три интервала:

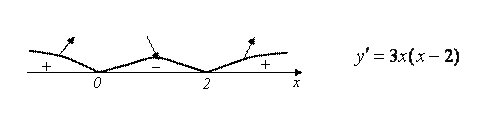
Определяем знаки производной в этих интервалах (они отмечены на рис. выше). Тем самым устанавливаем интервалы возрастания функции (они помечены стрелкой вверх) и интервал ее убывания (стрелка вниз), а также устанавливаем, что точка – точка максимума функции, а точка – точка ее минимума.

5. Находим (вычисляем) значения функции в точках ее максимума и минимума, устанавливая тем самым вершины и впадины графика функции:

; точка – вершина графика функции (округлая, т. к. ).

; точка – впадина графика функции (округлая, т. к. ).

6. В дополнение к проведенному исследованию найдем еще точки пересечения графика функции с осями координат:

А) С осью Ох:

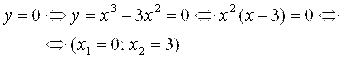
Б) С осью Оу:

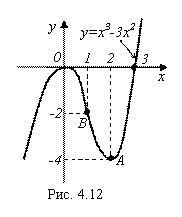
А теперь построим этот график (рис. 4.12):

 

 

< Предыдущая		Следующая >