4.05. Таблица производных основных элементарных функций
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5. ![]() ;
;
5* ![]() ;
;
6. 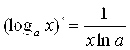 ;
;
6*.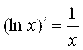 ;
;
7. ![]() ;
;
8. ![]() ;
;
9. 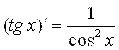 ;
;
10. 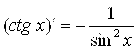 ;
;
11.  ;
;
12. 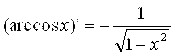 ; (2.1)
; (2.1)
13. 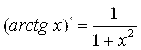 ;
;
14.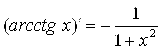 .
.
Таблицу производных желательно выучить наизусть.
Обратим внимание, что производные степенной и показательной функции (формулы 4 и 5) находятся по разным формулам; что из всех показательных функций ![]() наиболее простую производную имеет функция
наиболее простую производную имеет функция ![]() ; что из всех логарифмических функций
; что из всех логарифмических функций ![]() наиболее простую производную имеет натуральный логарифм
наиболее простую производную имеет натуральный логарифм ![]() .
.
Нахождение производных многих других элементарных функций (более сложных, не входящих в эту таблицу) осуществляется на основе следующих правил вычисления производных (Правил дифференцирования функций):
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5.  . (2.2)
. (2.2)
Здесь ![]() и
и ![]() – любые две дифференцируемые функции, а С – любая константа.
– любые две дифференцируемые функции, а С – любая константа.
Таблица производных (2.1) и правила дифференцирования (2.2) известны еще из курса школьной математики, поэтому их вывод, основанный на использовании определения производной (1.6), опускаем.
Пример 4. ![]() ;
; ![]()
![]()
Пример 5. ![]() ;
; ![]()
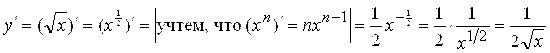 .
.
Полученный результат
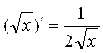 , (2.3)
, (2.3)
Наряду с формулами (2.1), полезно запомнить.
Пример 6. ![]() ;
; ![]()
Решение.
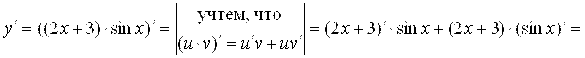
![]() .
.
Пример 7. ![]() ;
; ![]()
Решение.

Полученный результат
 (2.4)
(2.4)
Тоже полезно запомнить.
| < Предыдущая | Следующая > |
|---|