4.03. Связь между дифференцируемостью и непрерывностью функции
Теорема. Если функция ![]() дифференцируема в точке X, то она и непрерывна в этой точке. Обратное не гарантировано.
дифференцируема в точке X, то она и непрерывна в этой точке. Обратное не гарантировано.
Доказательство. Пусть функция ![]() Дифференцируема в точке X. Это значит, что ее производная
Дифференцируема в точке X. Это значит, что ее производная ![]() существует и конечна в точке X. То есть
существует и конечна в точке X. То есть

Существует и конечен. По определению предела это значит, что
 при
при ![]() .
.
То есть при малых ![]() имеем
имеем 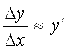 , откуда
, откуда ![]() , причем это приближенное равенство тем точнее, чем меньше
, причем это приближенное равенство тем точнее, чем меньше ![]() . Устремляя в нем
. Устремляя в нем ![]() , получаем, что и
, получаем, что и ![]() . А это, в силу (2.5) главы 3, и означает непрерывность функции
. А это, в силу (2.5) главы 3, и означает непрерывность функции ![]() в точке X. Первая часть теоремы доказана.
в точке X. Первая часть теоремы доказана.
Обратно, если функция ![]() непрерывна в некоторой точке X, то это еще не значит, что она дифференцируема в этой точке. Например, функция
непрерывна в некоторой точке X, то это еще не значит, что она дифференцируема в этой точке. Например, функция ![]() , график которой изображен на рис. 4.7, непрерывна в любой точке X, ибо её график сплошной (без разрывов). И тем не менее в точках X1, X2 и X3, как было показано выше, она не дифференцируема.
, график которой изображен на рис. 4.7, непрерывна в любой точке X, ибо её график сплошной (без разрывов). И тем не менее в точках X1, X2 и X3, как было показано выше, она не дифференцируема.
Упражнения
1. Опираясь на геометрический смысл производной показать, что
А) производная функции ![]() для любого X равна 2;
для любого X равна 2;
Б) производная функции ![]() для любого X равна 0;
для любого X равна 0;
В) производная функции ![]() для
для ![]() положительна, а для
положительна, а для ![]() отрицательна.
отрицательна.
2. Уравнение движения точки по ее траектории (рис. 4.3) имеет вид: ![]() . Показать, что точка тормозит при своем движении.
. Показать, что точка тормозит при своем движении.
3. Функция ![]() – уравнение кривой спроса (рис. 4.6). Показать, что для любых допустимых Q производная этой функции отрицательна.
– уравнение кривой спроса (рис. 4.6). Показать, что для любых допустимых Q производная этой функции отрицательна.
| < Предыдущая | Следующая > |
|---|