4.02. Дифференцируемость функции в точке и на промежутке
Производная функции, согласно ее математического определения (1.5) и (1.6) – это некий предел. Но, как и всякий предел, он может оказаться:
А) конечным; б) бесконечным; в) вообще не существовать.
Если для данного X имеет место вариант (а), то есть если при заданном X производная ![]() функции
функции ![]() Существует и конечна, то эта функция называется Дифференцируемой в точке x.
Существует и конечна, то эта функция называется Дифференцируемой в точке x.
Функция, дифференцируемая в Каждой точке X некоторого промежутка оси Ох (например, интервала (A; B) или отрезка [A; B]) называется Дифференцируемой на этом промежутке. Кстати, сама процедура вычисления производной функции называется ее Дифференцированием (продифференцировать функцию – это значит найти ее производную).
 Из геометрического смысла производной функции, определяемого равенством (1.11) и рис. 4.5, вытекают следующие два наглядные необходимые и достаточные условия дифференцируемости заданной функции
Из геометрического смысла производной функции, определяемого равенством (1.11) и рис. 4.5, вытекают следующие два наглядные необходимые и достаточные условия дифференцируемости заданной функции ![]() в заданной точке X:
в заданной точке X:
1) Существование касательной к графику функции в его точке с абсциссой X.
2) Невертикальность этой касательной (ибо ![]() не существует).
не существует).
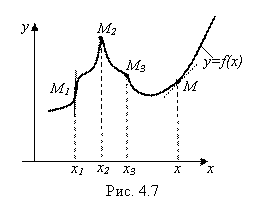
Например, функция ![]() , график которой изображен на рис. 4.7, не дифференцируема в точках X1, X2 и X3.
, график которой изображен на рис. 4.7, не дифференцируема в точках X1, X2 и X3.
Действительно, точке X1 соответствует на графике функции точка M1 с вертикальной касательной. Точке X2 (точке максимума функции) соответствует остроконечная вершина M2, касательная в которой не существует. Точке X3 соответствует точка M3 – точка излома графика функции, в которой тоже касательная не существует.
Во всех же остальных точках M графика функции касательную к графику провести можно, и она невертикальна. Значит, для всех остальных X, отличных от (X1; X2; X3), существует производная функции. То есть во всех остальных точках X функция ![]() дифференцируема.
дифференцируема.
| < Предыдущая | Следующая > |
|---|