3.7. Бесконечно малые функции и их сравнение

Пусть и – некоторые две функции, а X стремится к некоторому (конечному или бесконечному). Если при этом и , то есть если

и , (4.1)

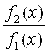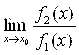То обе эти функции называются Бесконечно малыми при . Возникает вопрос: как их сравнить (кто меньше?). Ответ на этот вопрос мы получим, если исследуем отношение этих функций при , то есть найдем . При этом возможны следующие варианты.

Вариант 1:

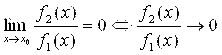при (4.2)

Это значит, что несравненно меньше при ( несравненно быстрее, чем , стремится к нулю при ). В этом случае говорят, что функция является Бесконечно малой функцией более высокого (высшего) порядка малости, чем функция , При . И обозначают этот факт так:

при (4.3)

(читается: есть «О малое» от при ). Суть записи (4.3) состоит, как сказано выше, в том, что бесконечно малая функция является бесконечно малой частью другой бесконечно малой функции при .

Вариант 2:

при (4.4)

Это значит, что при бесконечно малые функции и практически не отличаются друг от друга. В этом случае говорят, что Функция эквивалентна (равносильна) функции при . И обозначается это так:

при (4.5)

(~ – знак эквивалентности).

Вариант 3:

при , (4.6)

Где А – конечное число, не равное ни нулю, ни единице (эти два случая мы рассмотрели выше). Тогда, очевидно,

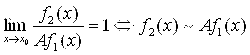при . (4.7)

В этом случае говорят, что бесконечно малые при функции и – Одного порядка малости. И записывают этот факт так:

при (4.8)

(читается: есть «О большое» от при ).

Вариант 4:

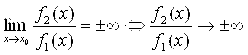при , (4.9)

Тогда

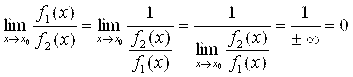
А это значит, что при .

Пример 1. Показать, что

А) при (X – в радианах); б) при ;

В) при ; г) при (X – в радианах);

Д) при ; е) при ;

Ж) при . (4.10)

Решение. Эквивалентность (4.5) означает выполнение предельного равенства (4.4). Поэтому для подтверждения эквивалентностей (а)-(ж) вычислим необходимые пределы (4.4) и покажем, что все они равны 1:

А) – согласно (2.7);

Б) 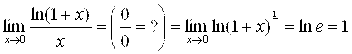– согласно (2.7);

В) ;

Г) ;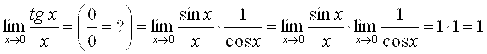

Д)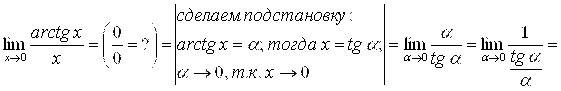

;

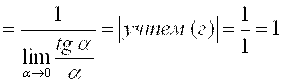Е)

;

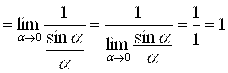Ж)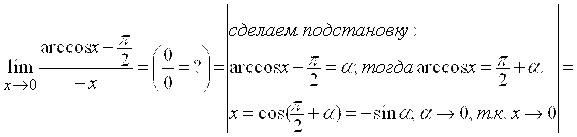

.

Итак, все эквивалентности(4.10) доказаны.

< Предыдущая		Следующая >