3.6. Нахождение невертикальных асимптот

Рассматривая рис. 3.14, приходим к очевидному выводу: если некоторая линия L с уравнением является невертикальной асимптотой графика функции при или при , то это значит, что при таком изменении X функция , то есть , а значит

, где при или при . (3.2)

И обратно, при выполнении (3.2) функция – асимптота функции . В частности, если

, где при или при , (3.3)

То соответственно при или при горизонтальная прямая будет асимптотой графика функции .

Пример 2. Найти невертикальные асимптоты графика функции

.

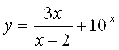Решение. Для их нахождения нужно выяснить поведение функции Y При и при .

А) Если , то очевидно, что

; .

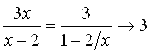Поэтому при функция . А это значит, что линия L с уравнением является асимптотой графика нашей функции при .

Б) Если , то очевидно, что

; .

Поэтому при наша функция . А это значит, что при асимптотой графика нашей функции Y является горизонтальная прямая .

Пример 3. Определить все имеющиеся асимптоты графика функции и изобразить поведение этого графика возле его асимптот.

Решение. Начнем с нахождения области определения функции Y. Функция определена, а следовательно, и непрерывна для всех X, кроме . То есть – единственная точка разрыва нашей функции. А значит, вертикальная прямая , проходящая через эту точку – единственная возможная вертикальная асимптота графика нашей функции.

Проверим, действительно ли она – вертикальная асимптота. Для этого выясним, в соответствии с (3.1), поведение функции Y при и при :

;

То есть При и при . А это значит, что вертикальная прямая является асимптотой графика функции Y, причем и при , и при .

Теперь поищем возможные невертикальные асимптоты. Для этого рассмотрим поведение функции Y при и при .

А) Если , то

.

Учтем, что (это устанавливается делением на «в столбик»). То есть

, где , .

И так как при , а при к нулю не стремится, то при наша функция 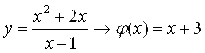. А это, в соответствии с (3.2), означает, что линия с уравнением (прямая) является асимптотой графика нашей функции Y при .

Б) Если , то буквально повторяя (а), приходим к выводу, что прямая является асимптотой графика нашей функции и при .

Теперь изобразим график нашей функции вместе с его асимптотами. Для более качественного построения этого графика найдем еще точки его пересечения с осями координат.

1) С осью Ох:

.

2) С осью Оу:

.

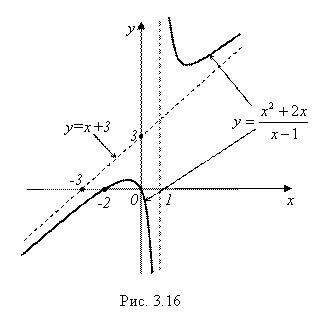
А теперь строим график (рис. 3.16).

Упражнения

Найти асимптоты графиков функций

А) ; б) ; в)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

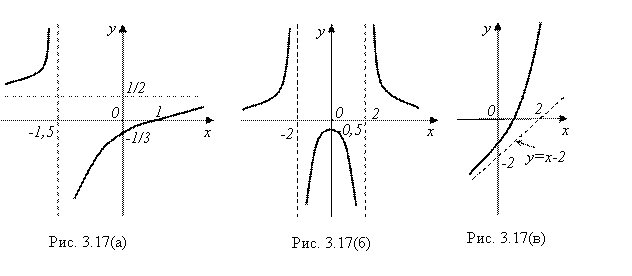
И построить эти графики вместе с их асимптотами.

Ответ: - см. рис. 3.17 (а) – (в).

< Предыдущая		Следующая >