3.5. Нахождение вертикальных асимптот
Рисунок 3.14 свидетельствует: если прямая ![]() – вертикальная асимптота графика функции
– вертикальная асимптота графика функции ![]() , то должны выполняться два условия:
, то должны выполняться два условия:
1) A – точка разрыва функции ![]() ; (3.1)
; (3.1)
2) ![]() (+¥ или –¥) или
(+¥ или –¥) или ![]() (+¥ или –¥).
(+¥ или –¥).
И обратно, если выполняются оба условия (3.1), то прямая ![]() – вертикальная асимптота графика функции
– вертикальная асимптота графика функции ![]() .
.
Из сказанного вытекает следующая Схема нахождения вертикальных асимптот графика функции ![]() :
:
1) Находим все точки разрыва (А1; А2; …) функции, то есть те изолированные точки оси Ох, в которых функция не определена (ибо там, где элементарная функция определена, там она и непрерывна).
2) Каждую из точек разрыва проверяем на выполнимость второго условия (3.1).
Пример 1. Найти вертикальные асимптоты графика функции
![]()
И сделать геометрическую иллюстрацию полученного результата.
Решение. Данная функция не определена, а следовательно, разрывна лишь в двух точках оси Ох: ![]() и
и ![]() . Проверим каждую из них на выполнимость второго условия (3.1):
. Проверим каждую из них на выполнимость второго условия (3.1):
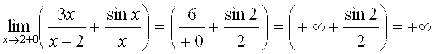

 ;
;  .
.
Второе условие (3.1) выполняется для точки ![]() и не выполняется для точки
и не выполняется для точки ![]() . Значит, лишь прямая
. Значит, лишь прямая ![]() является вертикальной асимптотой графика нашей функции, причем и при
является вертикальной асимптотой графика нашей функции, причем и при ![]() , и при
, и при ![]() . А прямая
. А прямая ![]() (ось Оу) вертикальной асимптотой графика функции не является. Геометрическая иллюстрация полученных результатов дана на рис. 3.15.
(ось Оу) вертикальной асимптотой графика функции не является. Геометрическая иллюстрация полученных результатов дана на рис. 3.15.
 На этом рисунке представлено лишь то, что выяснено выше: поведение функции Y возле ее точек разрыва
На этом рисунке представлено лишь то, что выяснено выше: поведение функции Y возле ее точек разрыва ![]() и
и ![]() . Вдали от этих точек мы эту функцию не исследовали, поэтому ее график не известен (он лишь намечен пунктирной линией).
. Вдали от этих точек мы эту функцию не исследовали, поэтому ее график не известен (он лишь намечен пунктирной линией).
| < Предыдущая | Следующая > |
|---|