3.3. Предел функции. Непрерывность и разрывы функций
Пусть ![]() – некоторая функция, рассматриваемая на некотором числовом множестве оси Ох (например, на отрезке
– некоторая функция, рассматриваемая на некотором числовом множестве оси Ох (например, на отрезке ![]() или на интервале
или на интервале ![]() этой оси). И пусть X0 – некоторая внутренняя или граничная точка этого множества. Для отрезка
этой оси). И пусть X0 – некоторая внутренняя или граничная точка этого множества. Для отрезка ![]() такой точкой X0 может быть любая точка этого отрезка. А для интервала
такой точкой X0 может быть любая точка этого отрезка. А для интервала ![]() – любая точка этого интервала, включая не принадлежащие ему его границы A и B.
– любая точка этого интервала, включая не принадлежащие ему его границы A и B.
Будем рассматривать значения функции ![]() для аргумента X, последовательно принимающего некоторые значения (X1; X2; …Xn; …), выбранные таким образом, что
для аргумента X, последовательно принимающего некоторые значения (X1; X2; …Xn; …), выбранные таким образом, что ![]() . При этом может оказаться, что соответствующая последовательность значений (Y1; Y2; …Yn; …) функции
. При этом может оказаться, что соответствующая последовательность значений (Y1; Y2; …Yn; …) функции ![]() стремится к некоторому конечному или бесконечному Y0 (
стремится к некоторому конечному или бесконечному Y0 (![]() ). И если это стремление Y к Y0 осуществляется При любом способе стремления X к X0, то число Y0 называется Пределом функции
). И если это стремление Y к Y0 осуществляется При любом способе стремления X к X0, то число Y0 называется Пределом функции ![]() при
при ![]() . И записывается это так:
. И записывается это так:
![]() (2.1)
(2.1)
(читается: предел функции ![]() при
при ![]() равен Y0). Обратно, равенство (2.1) означает, что при
равен Y0). Обратно, равенство (2.1) означает, что при ![]() функция
функция ![]() . Причем стремление Y к Y0 осуществляется При любом способе стремления X к X0.
. Причем стремление Y к Y0 осуществляется При любом способе стремления X к X0.
Отметим, что если X0 – граничная точка числового множества оси Ох, на котором рассматривается функция ![]() (крайняя левая или крайняя правая его точка), то X может стремиться к X0 либо только справа, либо только слева. Такое стремление X к X0 обозначают соответственно
(крайняя левая или крайняя правая его точка), то X может стремиться к X0 либо только справа, либо только слева. Такое стремление X к X0 обозначают соответственно ![]() (X стремится к X0 справа) и
(X стремится к X0 справа) и ![]() (X стремится к X0 слева) – рис. 3.4.
(X стремится к X0 слева) – рис. 3.4.
А соответствующие пределы функции ![]() называют соответственно пределами справа и слева:
называют соответственно пределами справа и слева:
![]() – предел функции
– предел функции ![]() при
при ![]() справа; (2.2)
справа; (2.2)
![]() – предел функции
– предел функции ![]() при
при ![]() слева.
слева.
Такие пределы функции называются Односторонними.
Если X0 – внутренняя точка числового множества оси Ох, на котором рассматривается функция ![]() , то для нее можно искать оба односторонних предела – и предел справа (при
, то для нее можно искать оба односторонних предела – и предел справа (при ![]() ), и предел слева (при
), и предел слева (при ![]() ). Кроме того, можно искать и общий (двусторонний) предел (2.1). Очевидно, что если этот двусторонний предел существует и равен Y0, то существуют и оба односторонних, и оба они равны Y0. Обратно, если оба односторонних предела (2.2) существуют и равны, то существует и равен им и двусторонний предел (2.1).
). Кроме того, можно искать и общий (двусторонний) предел (2.1). Очевидно, что если этот двусторонний предел существует и равен Y0, то существуют и оба односторонних, и оба они равны Y0. Обратно, если оба односторонних предела (2.2) существуют и равны, то существует и равен им и двусторонний предел (2.1).
Суть пределов функции, как двустороннего, так и односторонних, можно наглядно проиллюстрировать. В частности, сделаем это для двустороннего предела (2.1).
Согласно определению этого предела, при любом способе стремления X к X0 соответствующее значение функции ![]() стремится к Y0. То есть если X подойдет достаточно близко к X0, то и
стремится к Y0. То есть если X подойдет достаточно близко к X0, то и ![]() подойдет достаточно близко к Y0. Иначе говоря, как бы ни была мала
подойдет достаточно близко к Y0. Иначе говоря, как бы ни была мала ![]() -окрестность
-окрестность ![]() точки Y0, должна найтись такая соответствующая ей
точки Y0, должна найтись такая соответствующая ей ![]() -окрестность
-окрестность ![]() точки X0, что как только X в своем стремлении к X0 попадет в
точки X0, что как только X в своем стремлении к X0 попадет в ![]() -окрестность точки X0, соответствующее этому X значение функции
-окрестность точки X0, соответствующее этому X значение функции ![]() попадет в
попадет в ![]() -окрестность точки Y0 (рис. 3.5).
-окрестность точки Y0 (рис. 3.5).
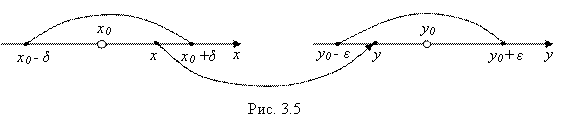
Для иллюстрации же односторонних пределов (2.2) в рис. 3.5 нужно заменить двустороннюю ![]() -окрестность точки X0 на соответствующую одностороннюю
-окрестность точки X0 на соответствующую одностороннюю ![]() или
или ![]() .
.
Теперь перейдем к рассмотрению такого важнейшего понятия, как Непрерывность функции.
Если функция ![]() определена для всех X из некоторого отрезка
определена для всех X из некоторого отрезка ![]() или интервала
или интервала ![]() оси Ох, и ее график для указанных Х – сплошная (непрерывная) линия, то такая функция называется Непрерывной на этом отрезке или интервале. Непрерывная на отрезке или интервале функция считается непрерывной в любой конкретной точке X0 этого отрезка или интервала.
оси Ох, и ее график для указанных Х – сплошная (непрерывная) линия, то такая функция называется Непрерывной на этом отрезке или интервале. Непрерывная на отрезке или интервале функция считается непрерывной в любой конкретной точке X0 этого отрезка или интервала.
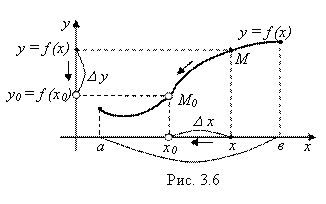 Если функция
Если функция ![]() непрерывна в некоторой точке X0, то очевидно, что при
непрерывна в некоторой точке X0, то очевидно, что при ![]() значение функции
значение функции ![]() (рис. 3.6). Причем это стремление Y к Y0 при
(рис. 3.6). Причем это стремление Y к Y0 при ![]() будет иметь место и при
будет иметь место и при ![]() , и
, и ![]() . Действительно, стремление X к X0 вызывает для непрерывной функции стремление (приближение) точки M к точке М0, а значит, и стремление ординаты Y точки М к ординате Y0 точки М0, с какой бы стороны от точки М0 ни находилась точка М.
. Действительно, стремление X к X0 вызывает для непрерывной функции стремление (приближение) точки M к точке М0, а значит, и стремление ординаты Y точки М к ординате Y0 точки М0, с какой бы стороны от точки М0 ни находилась точка М.
Стремление ![]() к
к ![]() при
при ![]() означает, что
означает, что
![]() (2.3)
(2.3)
Если ввести обозначения (см. рис. 3.6)
![]()
![]() – приращение аргумента X в точке X0;
– приращение аргумента X в точке X0;
![]() – приращение функции
– приращение функции ![]() в точке X0, (2.4)
в точке X0, (2.4)
То стремление ![]() К
К ![]() при
при ![]() , то есть выполнение равенства (2.3), означает, что
, то есть выполнение равенства (2.3), означает, что ![]() при
при ![]() . И обратно, если при
. И обратно, если при ![]() и
и ![]() , то это означает, что при аргументе
, то это означает, что при аргументе ![]() функция
функция ![]() , а значит, выполняется равенство (2.3). Таким образом, условие
, а значит, выполняется равенство (2.3). Таким образом, условие
![]() при
при ![]() (
(![]() ) (2.5)
) (2.5)
И условие (2.3) равносильны. Оба они, в разной форме, представляют собой Математическое определение непрерывности функции ![]() в заданной точке X0.
в заданной точке X0.
Если условие непрерывности (2.3) (или равносильное ему (2.5)) функции ![]() в некоторой точке X0 не выполняется, то функция называется Разрывной в точке X0. А сама такая точка X0 называется Точкой разрыва функции
в некоторой точке X0 не выполняется, то функция называется Разрывной в точке X0. А сама такая точка X0 называется Точкой разрыва функции ![]() . Например, точка X0 Является точкой разрыва функции
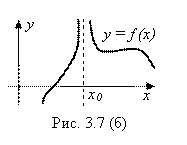
. Например, точка X0 Является точкой разрыва функции ![]() И на рис. 3.7(а), и на рис. 3.7(б), и на рис. 3.7(в).
И на рис. 3.7(а), и на рис. 3.7(б), и на рис. 3.7(в).
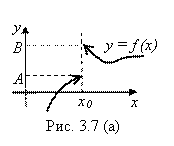

Действительно, для рис. 3.7 (а) условие непрерывности (2.3) не выполняется сразу по двум причинам:
1) ![]() – не существует; 2)
– не существует; 2) ![]() ;
; ![]() ;
; ![]() , значит,
, значит, ![]() – не существует.
– не существует.
Для рис. 3.7 (б) условие непрерывности (2.3) тоже, очевидно, не выполняется. Действительно,
![]() (существует, хоть и не является конечным числом), но
(существует, хоть и не является конечным числом), но ![]() – не существует.
– не существует.
На рис. 3.7 (в) из сплошного (непрерывного) графика функции ![]() вырезана точка М0 и перемещена по вертикали в другое положение М. В итоге точка X0 станет точкой разрыва функции
вырезана точка М0 и перемещена по вертикали в другое положение М. В итоге точка X0 станет точкой разрыва функции ![]() , ибо для неё получаем:
, ибо для неё получаем:
1) ![]() – существует; 2)
– существует; 2) ![]() – существует; 3) Однако
– существует; 3) Однако ![]() , то есть
, то есть ![]() . Если вернуть точку М на место (в точку М0), то функция
. Если вернуть точку М на место (в точку М0), то функция ![]() опять станет непрерывной в точке X0. Поэтому разрыв этой функции в точке X0 , изображенный на рис. 3.7 (в), называется Устранимым.
опять станет непрерывной в точке X0. Поэтому разрыв этой функции в точке X0 , изображенный на рис. 3.7 (в), называется Устранимым.
Рисунки 3.7 (а)-(в) наглядно иллюстрируют суть точек разрыва функций. А именно, Точкой разрыва данной функции ![]() является такое значение X0 аргумента X этой функции, при котором нарушается сплошность (непрерывность) ее графика.
является такое значение X0 аргумента X этой функции, при котором нарушается сплошность (непрерывность) ее графика.
Вспомним, что графики основных элементарных функций (линейной ![]() , квадратичной
, квадратичной ![]() , обратно-пропорциональной зависимости
, обратно-пропорциональной зависимости ![]() и т. д.) являются сплошными (непрерывными) линиями для всех X, для которых эти функции определены. И разрыв указанные линии терпят лишь при тех значениях
и т. д.) являются сплошными (непрерывными) линиями для всех X, для которых эти функции определены. И разрыв указанные линии терпят лишь при тех значениях ![]() , при которых соответствующие им функции не определены. Такие X0 и являются точками разрыва элементарных функций.
, при которых соответствующие им функции не определены. Такие X0 и являются точками разрыва элементарных функций.
Например, квадратичная функция ![]() определена для любых X. И ее график (парабола) является сплошной (непрерывной) линией при любых X. То есть точек разрыва у функции
определена для любых X. И ее график (парабола) является сплошной (непрерывной) линией при любых X. То есть точек разрыва у функции ![]() нет. А вот функция
нет. А вот функция ![]() определена для любых X, кроме
определена для любых X, кроме ![]() . И соответственно ее график (гипербола) является сплошной (непрерывной) линией для любых X, кроме
. И соответственно ее график (гипербола) является сплошной (непрерывной) линией для любых X, кроме ![]() , где она терпит разрыв (рис. 3.8 (а) и 3.8 (б)).
, где она терпит разрыв (рис. 3.8 (а) и 3.8 (б)).
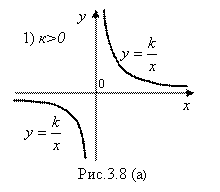
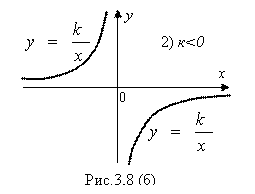
Указанным выше свойством основных элементарных функций обладают, как можно доказать, и любые конечные комбинации этих функций (их суммы, произведения, функции от функций, то есть сложные функции и т. д.). То есть любые функции ![]() , составленные из основных элементарных функций (а с другими функциями, собственно говоря, мы встречаться практически и не будем) Будут непрерывны для всех значений аргумента X, для которых они определены. А следовательно, Точками их разрыва будут лишь те отдельные изолированные точки X0, в которых они не определены. Изолированные – это значит такие точки X0, что в любой окрестности [
, составленные из основных элементарных функций (а с другими функциями, собственно говоря, мы встречаться практически и не будем) Будут непрерывны для всех значений аргумента X, для которых они определены. А следовательно, Точками их разрыва будут лишь те отдельные изолированные точки X0, в которых они не определены. Изолированные – это значит такие точки X0, что в любой окрестности [![]() ;
;![]() ] этих точек функция определена, и лишь в самих точках X0 она не определена.
] этих точек функция определена, и лишь в самих точках X0 она не определена.
Например, функция

Определена, а следовательно, и непрерывна для любых X, кроме точек ![]() и
и ![]() . В окрестности каждой из этих точек функция определена, и только в самих этих точках она не определена. Значит, эти точки
. В окрестности каждой из этих точек функция определена, и только в самих этих точках она не определена. Значит, эти точки ![]() и
и ![]() и есть точки разрыва данной функции Y.
и есть точки разрыва данной функции Y.
Выясним, заодно, и характер поведения этой функции возле каждой из ее точек разрыва – и справа, и слева.
1) Пусть ![]() ; тогда
; тогда 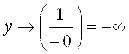 ;
; ![]() .
.
2) Пусть ![]() ; тогда
; тогда 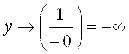 ;
; ![]() .
.
3) Пусть ![]() ; тогда
; тогда 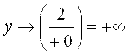 ;
; ![]() .
.
4) Пусть ![]() ; тогда
; тогда 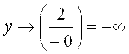 ;
; ![]() .
.
Отобразив установленное поведение функции Y возле ее точек разрыва, получим важные фрагменты графика функции (они изображены на рис. 3.9 сплошными линиями). 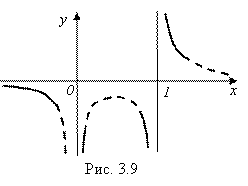 Другие же элементы графика функции (обозначенные пунктиром) требуют для своего детального изображения дополнительного исследования. Но об этом поговорим позже, когда будет рассмотрена полная схема исследования функций (глава 4, § 3).
Другие же элементы графика функции (обозначенные пунктиром) требуют для своего детального изображения дополнительного исследования. Но об этом поговорим позже, когда будет рассмотрена полная схема исследования функций (глава 4, § 3).
Рассмотрим теперь несколько примеров вычисления пределов функций.
Пример 1. Найти ![]() .
.
Решение. Функция ![]() определена, а следовательно, и непрерывна в любой точке
определена, а следовательно, и непрерывна в любой точке ![]() , в том числе и в точке
, в том числе и в точке ![]() . Поэтому, пользуясь равенством (2.3) для непрерывных функций, получаем:
. Поэтому, пользуясь равенством (2.3) для непрерывных функций, получаем:
![]()
Впрочем, этот результат и так очевиден, ибо, естественно, при ![]() функция
функция ![]() .
.
Пример 2. Найти ![]() .
.
Решение. Функция ![]() определена, а следовательно, и непрерывна для всех X, кроме
определена, а следовательно, и непрерывна для всех X, кроме ![]() . То есть
. То есть ![]() – точка разрыва этой функции. Поэтому найти искомый предел при
– точка разрыва этой функции. Поэтому найти искомый предел при ![]() по формуле (2.3), которая применяется лишь для непрерывных в точке X0 функций, нельзя. Но это в данном случае и не важно – значение предела и так очевидно. Действительно, совершенно очевидно, что при любом способе стремления
по формуле (2.3), которая применяется лишь для непрерывных в точке X0 функций, нельзя. Но это в данном случае и не важно – значение предела и так очевидно. Действительно, совершенно очевидно, что при любом способе стремления ![]() функция
функция ![]() . То есть
. То есть
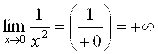 .
.
Пример 3. Найти 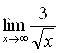 .
.
Решение. При ![]() функция
функция 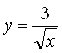 , очевидно, стремится к нулю. Поэтому
, очевидно, стремится к нулю. Поэтому
 .
.
Пример 4. Найти ![]() .
.
Решение. Как и в примере 2, воспользоваться равенством (2.3) здесь нельзя, так как ![]() – точка разрыва функции
– точка разрыва функции ![]() . Однако очевидно, что при
. Однако очевидно, что при ![]() функция
функция ![]() , а при
, а при ![]() функция
функция ![]() . То есть односторонние пределы типа (2.2) здесь разные:
. То есть односторонние пределы типа (2.2) здесь разные:
 ;
;  .
.
А значит, общий ![]() не существует.
не существует.
Пример 5. Найти  .
.
Решение. Воспользоваться равенством (2.3) и здесь нельзя, так как при ![]() функция
функция  не определена (при
не определена (при ![]() выражение
выражение 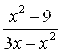 дает неопределенное выражение
дает неопределенное выражение ![]() ). Значит, как и в примерах (2) – (4), нужно анализировать поведение функции при
). Значит, как и в примерах (2) – (4), нужно анализировать поведение функции при ![]() .
.
Функция  представляет собой дробь, у которой при
представляет собой дробь, у которой при ![]() и числитель, и знаменатель одновременно стремятся к нулю. Но стремление числителя дроби к нулю ведет к уменьшению этой дроби, а стремление знаменателя к нулю – наоборот, к ее увеличению. Какой фактор перевесит – пока неясно, в разных случаях бывает по-разному. То есть в данном пределе имеется неясность (неопределенность) типа
и числитель, и знаменатель одновременно стремятся к нулю. Но стремление числителя дроби к нулю ведет к уменьшению этой дроби, а стремление знаменателя к нулю – наоборот, к ее увеличению. Какой фактор перевесит – пока неясно, в разных случаях бывает по-разному. То есть в данном пределе имеется неясность (неопределенность) типа ![]() . Кстати, это не единственный возможный тип неопределенности, но о прочих типах – позже.
. Кстати, это не единственный возможный тип неопределенности, но о прочих типах – позже.
Неопределенность, встретившуюся при вычислении предела, нужно Раскрывать. То есть как-то так преобразовать выражение под знаком предела, чтобы неопределенность исчезла и предел стал очевиден. В частности, раскроем нашу неопределенность:
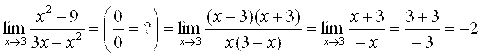
Пример 6. Найти ![]() .
.
Решение. Здесь при ![]() и числитель, и знаменатель дроби стремятся к бесконечности. Но стремление числителя дроби к бесконечности ведет к неограниченному росту дроби, а стремление знаменателя дроби к бесконечности, наоборот, ведет к неограниченному уменьшению дроби (к стремлению ее к нулю). Эти два фактора, как и в предыдущем примере, работают друг против друга, приводя к неопределенности типа
и числитель, и знаменатель дроби стремятся к бесконечности. Но стремление числителя дроби к бесконечности ведет к неограниченному росту дроби, а стремление знаменателя дроби к бесконечности, наоборот, ведет к неограниченному уменьшению дроби (к стремлению ее к нулю). Эти два фактора, как и в предыдущем примере, работают друг против друга, приводя к неопределенности типа ![]() . Раскроем её:
. Раскроем её:
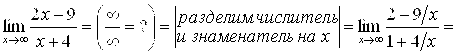
 .
.
Неопределенности типа ![]() и
и ![]() принадлежат к числу наиболее часто встречающихся при вычислении пределов неопределенностей. Но есть и другие типы неопределенностей. Всего этих типов семь:
принадлежат к числу наиболее часто встречающихся при вычислении пределов неопределенностей. Но есть и другие типы неопределенностей. Всего этих типов семь:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; (2.6)
; (2.6)
5) ![]() ; 6)
; 6) ![]() ; 7)
; 7)![]() .
.
Эти записи нужно понимать не буквально, не как арифметические операции с символами 0 и ¥, а как Предельные ситуации при вычислении пределов. Для сравнения приведем другие предельные ситуации, неопределенностями не являющиеся:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]()
(![]() ;
; ![]() ;
; ![]() ;
; ![]() )
)
5) ![]() ; 6)
; 6) ![]() .
.
Если при вычислении предела функции возникает какая-либо из неопределенностей (2.6), ее нужно как-то раскрывать. Если неопределенности нет, значит, ситуация ясная, и результат следует записать сразу.
Пример 7. Найти ![]() .
.
Решение.
![]()
Пример 8. Найти ![]() .
.
Решение.

Вычислению многих пределов, содержащих неопределенности, часто помогает использование двух так называемых Замечательных пределов:
1)  (X – угол в радианах) (2.7)
(X – угол в радианах) (2.7)
2) 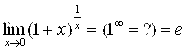 , где
, где ![]() .
.
Докажем первый замечательный предел. Для этого вспомним школьную формулу для длины L произвольной дуги окружности (рис. 3.10):
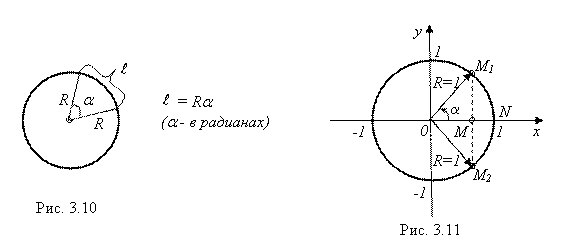
А теперь рассмотрим рис. 3.11:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; 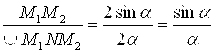 (
(![]() – в радианах).
– в радианах).
При ![]() хорда M1M2 и дуга M1NM2, неограниченно уменьшаясь, практически становятся неразличимыми (малая дуга практически не отличается от стягивающей ее хорды). То есть их отношение стремится к единице. Таким образом, при
хорда M1M2 и дуга M1NM2, неограниченно уменьшаясь, практически становятся неразличимыми (малая дуга практически не отличается от стягивающей ее хорды). То есть их отношение стремится к единице. Таким образом, при ![]() дробь
дробь ![]() . А это и означает, что
. А это и означает, что
![]() (
(![]() – угол в радианах)
– угол в радианах)
Полученный результат совпадает (при другом обозначении) с первым замечательным пределом (2.7).
Второй замечательный предел, приводящий к важному для всей высшей математики числу E (к Неперову числу – по имени шотландского математика 16–го века Джона Непера, введшего в математику это число), оставим без доказательства.
Число ![]() , как и число
, как и число ![]() , принадлежит к числу важнейших математических констант. А такие функции, как
, принадлежит к числу важнейших математических констант. А такие функции, как ![]() и
и ![]() , принадлежат к числу важнейших элементарных функций, используемых в высшей математике. Графики этих функций показаны на рисунках (3.12) и (3.13). При этом показательная функция
, принадлежат к числу важнейших элементарных функций, используемых в высшей математике. Графики этих функций показаны на рисунках (3.12) и (3.13). При этом показательная функция ![]() называется Экспоненциальной, а ее график называется Экспонентой. А логарифмическая функция
называется Экспоненциальной, а ее график называется Экспонентой. А логарифмическая функция ![]() называется Функцией натурального логарифма, а ее график называется Натуральной логарифмической кривой. Эти функции играют большую роль при математическом описании различного рода природных процессов. Именно поэтому, в частности, логарифм по основанию E назвали натуральным – от слова «natur» (природа).
называется Функцией натурального логарифма, а ее график называется Натуральной логарифмической кривой. Эти функции играют большую роль при математическом описании различного рода природных процессов. Именно поэтому, в частности, логарифм по основанию E назвали натуральным – от слова «natur» (природа).
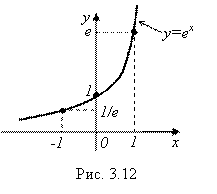
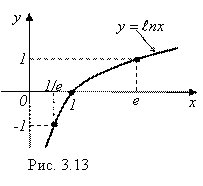
В математических справочниках имеются таблицы этих двух важных функций - и ![]() , и
, и ![]() . Впрочем, для вычисления натуральных логарифмов
. Впрочем, для вычисления натуральных логарифмов ![]() можно воспользоваться и таблицами общеизвестных десятичных логарифмов
можно воспользоваться и таблицами общеизвестных десятичных логарифмов ![]() , если применить формулу перехода в логарифмах от одного основания к другому:
, если применить формулу перехода в логарифмах от одного основания к другому:
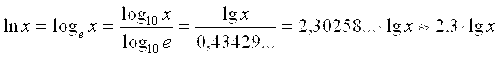 ;
;
![]() (2.8)
(2.8)
Пример 9. Найти  .
.
Решение.

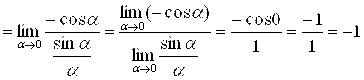 .
.
Пример 10. Найти  .
.
Решение.
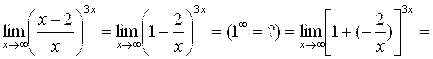
=| Введем обозначение: ![]() (
(![]() ); Тогда
); Тогда ![]() ;
; ![]() |=
|=
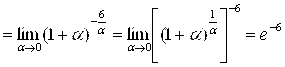 .
.
Пример 11. Найти ![]() .
.
Решение.
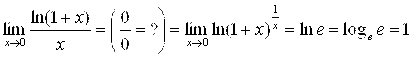 .
.
Упражнения
1. Найти ![]() . Указание: положить
. Указание: положить ![]() . Ответ: 1.
. Ответ: 1.
2. Найти 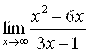 . Ответ:
. Ответ: ![]() .
.
3. Найти ![]() . Указание: положить
. Указание: положить ![]() . Ответ:
. Ответ: ![]() .
.
4. Найти ![]() . Ответ:
. Ответ: ![]() .
.
5. Найти  . Ответ:
. Ответ: ![]() .
.
6. Найти ![]() . Ответ: 0.
. Ответ: 0.
| < Предыдущая | Следующая > |
|---|