3.2. Основные свойства переменных величин и их пределов
Указанные ниже свойства практически очевидны, хотя их можно и строго доказать.
1) Если ![]() (переменная X неизменна и равна постоянной A), то естественно считать, что и
(переменная X неизменна и равна постоянной A), то естественно считать, что и ![]() . То есть предел постоянной равен ей самой:
. То есть предел постоянной равен ей самой:
![]() (1.5)
(1.5)
2) Если ![]() ,
, ![]() и A и B конечны, то
и A и B конечны, то ![]() . То есть
. То есть
![]() (1.6)
(1.6)
(предел суммы или разности переменных равен сумме или разности их пределов).
3) Если ![]() ,
, ![]() и A и B конечны, то
и A и B конечны, то ![]() . То есть
. То есть
![]() (1.7)
(1.7)
(предел произведения переменных равен произведению их пределов).
4) Если ![]() ,
, ![]() , A и B конечны и
, A и B конечны и ![]() , то
, то  . То есть
. То есть
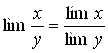 (1.8)
(1.8)
(предел частного равен частному пределов).
5) Если ![]() ,
, ![]() и
и ![]() – любые постоянные числа, то
– любые постоянные числа, то ![]() . То есть
. То есть
![]() (1.9)
(1.9)
Действительно, на основании предыдущих свойств имеем:
![]() .
.
6) Если X – бесконечно малая переменная величина (![]() ), то
), то ![]() – бесконечно большая переменная величина (
– бесконечно большая переменная величина (![]() ).
).
7) Если X – бесконечно большая переменная величина (![]() ), то
), то ![]() – бесконечно малая переменная величина (
– бесконечно малая переменная величина (![]() ).
).
8) Если переменная X ограничена (это значит, что все ее значения Xn расположены в некотором конечном числовом промежутке ![]() ), а переменная Y бесконечно малая (
), а переменная Y бесконечно малая (![]() ), то переменная
), то переменная ![]() – тоже бесконечно малая (
– тоже бесконечно малая (![]() ).
).
9) Если переменная X ограничена, а переменная Y бесконечно большая (![]() ), то переменная
), то переменная ![]() – бесконечно малая (
– бесконечно малая (![]() ).
).
10) Теорема Вейерштрасса.
А) Пусть значения Xn переменной X монотонно возрастают и при этом все они меньше некоторой постоянной величины C. Такая переменная X называется Монотонно возрастающей и ограниченной сверху (числом C). Она заведомо имеет конечный предел A, причем ![]() . Наглядную иллюстрацию этой ситуации дает рис. 3.2.
. Наглядную иллюстрацию этой ситуации дает рис. 3.2.

|
|

Упражнения
1.  (N = 1, 2, 3,…). Развернуть эту последовательность значений переменной X и найти ее предел.
(N = 1, 2, 3,…). Развернуть эту последовательность значений переменной X и найти ее предел.
Ответ: 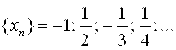 ;
; ![]() .
.
2. ![]() . Найти
. Найти ![]() .
.
Ответ: 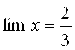 .
.
3.  (N = 1, 2, 3,…). Найти
(N = 1, 2, 3,…). Найти ![]() .
.
Ответ: ![]() .
.
| < Предыдущая | Следующая > |
|---|