3.1. Предел

Предел – это одно из самых фундаментальных понятий высшей математики. В данной главе мы рассмотрим две основные разновидности пределов: 1) предел переменной; 2) предел функции.

Пусть X – Переменная величина. Это значит, что величина X меняет свои значения. Этим она принципиально отличается от любой Постоянной величины A, которая своего неизменного значения не меняет. Например, высота столба – величина постоянная, а высота живого растущего дерева – величина переменная.

Переменная величина X считается заданной, если задана последовательность

(1.1)

Ее значений. То есть тех значений X1; X2; X3;…, которые она последовательно, одно за другим, принимает в процессе своего изменения. Будем считать, что этот процесс изменения величиной X своих значений ни на каком этапе не прекращается (переменная Х никогда не застывает, она «всегда живая»). А это значит, что последовательность (1.1) имеет бесконечное число значений, что и отмечено в (1.1) многоточием.

Естественно, возникает интерес относительно характера изменения величиной X своих значений. То есть возникает вопрос: меняются эти значения бессистемно, хаотически или все же как-то целенаправленно.

Основной интерес представляет, конечно, второй вариант. А именно, пусть значения Xn Переменной X по мере увеличения их номера N неограниченно приближаются (Стремятся) к некоторому конкретному числу A. Это значит, что разность (расстояние) между значениями Xn Переменной X и числом A сокращается, стремясь при увеличении N (при ) к нулю. Заменяя слово «стремится» стрелкой, сказанное выше можно записать так:

при <=> при (1.2)

Если имеет место (1.2), то говорят, что Переменная х стремится к числу а. Это число А Называется Пределом переменной X. И записывается это следующим образом:

<=> (1.3)

Читается: Предел X равен A (X стремится к A).

Стремление переменной X к своему пределу A Можно наглядно проиллюстрировать на числовой оси. Точный математический смысл этого стремления X к A состоит в том, что какое бы малое положительное число ни взять, а значит, каким бы малым промежутком ни окружить на числовой оси число A, в этот промежуток (в так называемую -окрестность числа A) попадут, начиная с некоторого номера N, все значения Xn Переменной X. В частности, на рис. 3.1 в изображенную -окрестность числа A попали все значения Xn Переменной X, начиная с номера .

Переменная X, имеющая своим пределом нуль (то есть стремящаяся к нулю) называется Бесконечно малой. А переменная X, неограниченно растущая по абсолютной величине, называется Бесконечно большой (ее модуль стремится к бесконечности).

Итак, если , то X – бесконечно малая переменная величина, а если , то X – бесконечно большая переменная величина. В частности, если или , то X – бесконечно большая переменная величина.

Если , то . И обратно, если , то . Отсюда получаем следующую важную связь между переменной X и ее пределом A:

(1.4)

Отметим, что не всякая переменная X имеет предел. У многих переменных нет предела. Есть он или нет – это зависит от того, какова последовательность (1.1) значений этой переменной.

Пример 1. Пусть

Здесь, очевидно, , то есть .

Пример 2. Пусть

Здесь, очевидно, , то есть . Значит, переменная X – бесконечно малая.

Пример 3. Пусть

Здесь, очевидно, , то есть . Значит, переменная X – бесконечно большая.

Пример 4. Пусть

Здесь, очевидно, переменная X ни к чему не стремится. То есть предела у нее нет ( не существует).

Пример 5. Пусть

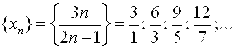
Здесь ситуация с пределом переменной X не так очевидна, как в предыдущих четырех примерах. Для прояснения этой ситуации преобразуем значения Xn переменной X:

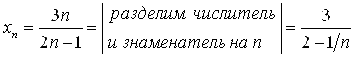
Очевидно, что при . Значит,

при .

А это значит, что , то есть .

Пример 6. Пусть

Здесь последовательность {Xn} значений переменной X представляет собой бесконечную геометрическую прогрессию со знаменателем Q. Следовательно, предел переменной X – это предел бесконечной геометрической прогрессии.

А) Если , то, очевидно, при . А это значит, что ().

Б) Если , то . То есть в этом случае значения переменной X не меняются – они все время равны 1. Тогда и ее предел равен 1 ().

В) Если , то . В этом случае, очевидно, не существует.

Г) Если , то – бесконечно возрастающая положительная числовая последовательность. А значит, ().

Д) Если , то вводя обозначение , где , получим: – знакопеременная числовая последовательность с бесконечно возрастающими по абсолютной величине членами:

при

А значит, переменная X бесконечно большая. Но в силу знакопеременности ее членов она не стремится ни к +∞, ни к –∞ (предела не имеет).

< Предыдущая		Следующая >