2.6. Линейная модель международной бездефицитной торговли

Будем считать, что бюджеты (X1; X2; …Xn) N стран расходуются этими странами целиком на покупку товаров внутри страны и вне ее (так называемый торговый бюджет). И пусть Xij – сумма, на которую J-ая страна закупает товаров у I-ой страны. Тогда

(J = 1, 2,… N) (3.10)

– бюджет J-ой страны, а

(I = 1, 2,… N) (3.11)

– общая выручка I-ой страны от внутренней и внешней торговли. При торговом бездефицитном бюджете общая выручка страны и составляет ее бюджет. Поэтому

(I = 1, 2,… N) (3.12)

Далее, пусть

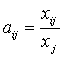(I,J = 1, 2,… N) (3.13)

– доля бюджета Xj, которую тратит J-ая страна на закупку товаров у I-ой страны. Тогда

(I,J = 1, 2,… N), (3.14)

Причем, в силу (3.10) и (3.13),

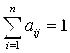(J = 1, 2,… N), (3.15)

Подставляя выражения (3.14) для Xij в выражения (3.11) для Pi и учитывая равенства (3.12), приходим к системе и линейных уравнений с N неизвестными (X1; X2; …Xn):

(I = 1, 2,… N), (3.16)

Или, в развернутой форме, к системе:

(3.17)

Матрица

(3.18)

Коэффициентов системы (3.18) называется Матрицей структурной торговли. Ее особенностью, согласно (3.15), является то, что сумма элементов каждого ее столбца равна единице, и все ее элементы неотрицательны. Если она задана, то решив систему (3.17), найдем бюджеты (X1; X2; …Xn) всех стран, принимающих участие в бездефицитной торговле.

Отметим, что система (3.17) является однородной. Действительно, перенеся правые части в (3.17) налево, получим следующую однородную систему

(3.19)

Сложив все уравнения этой системы, в силу равенств (3.15) получим тождество . Это значит, что каждое отдельное уравнение системы (3.19) можно выразить через другие ее уравнения. То есть каждое уравнение системы (3.19) является следствием остальных. Иначе говоря, оно автоматически будет выполняться, если будут выполняться остальные N–1 уравнений. Но это значит, что в системе (3.19) одно уравнение (любое!) можно отбросить. Тогда вместо квадратной системы (3.19) получим недоопределенную однородную систему. А недоопределенная система, как мы знаем из § 1, может или иметь бесчисленное множество решений, или не иметь их вообще. Но не иметь решений она не может, ибо заведомо одно решение (тривиальное) у нее есть: (; ; …; ). Значит, система (3.19) имеет бесчисленное множество решений. Чтобы из этого множества выделить искомое решение (X1; X2; …Xn), необходимо задать некоторое дополнительное условие для ее неизвестных, то есть для бюджетов Xi (I = 1, 2,… N) всех стран. Например, задать суммарный бюджет С Всех стран:

(3.20)

Пример 2. Структурная матрица торговли четырех стран имеет вид:

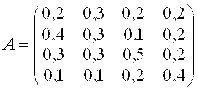
Найти бюджеты (X1; X2; X3; X4) этих стран, удовлетворяющие сбалансированной бездефицитной торговле при условии, что сумма бюджетов задана:

(усл. ед.).

Решение. Составим систему (3.19):

Отбросив в этой системе последнее уравнение и решив оставшуюся систему методом Гаусса (выкладки опускаем), получим:

; ; ; ,

Где T – свободный (произвольный) параметр. Подставив эти выражения в заданную сумму бюджетов, определим величину T:

Значит,

{; ; ; } (усл. ед.).

Упражнения

1. В таблице приведены данные об исполнении межотраслевого баланса за некоторый отчетный период в условных денежных единицах:

Отрасль производства	Производственное потребление	Конечный продукт	Валовой выпуск
1	2
1	100	160	240	500
2	275	40	85	400

Определить необходимый объем валового выпуска каждой отрасли, если конечный продукт первой отрасли должен увеличиться на 100 %, а второй отрасли – на 20 %.

Ответ: ;

2. Структурная матрица торговли трех стран имеет вид:

Найти бюджеты Этих стран, удовлетворяющие сбалансированной бездефицитной торговле при условии, что сумма их бюджетов равна 90 (усл. ед.).

Ответ: ; ; .

< Предыдущая		Следующая >