2.5. Межотраслевая модель Леонтьева
Предположим, что рассматривается N отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции, произведенной отраслью, идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.
Рассмотрим процесс производства за некоторый период времени (например, за год). Введем следующие обозначения:
Xi – общий (валовой) объем продукции I-ой отрасли (I = 1, 2,… N);
Xij – объем продукции I-ой отрасли, потребляемой J-ой отраслью в процессе производства (I,J = 1, 2,… N);
Yi –объем продукции I-ой отрасли для непроизводственного (личного и общественного) потребления (I = 1, 2,… N).
Указанные величины можно свести в таблицу:
|
Производственное |
Конечный продукт |
Валовой выпуск |
|
X11 X12 …… X1N X21 X22 …… X2N -------------------- Xn1 Xn2 …… Xnn |
Y1 Y2 ----- YN |
X1 X2 ----- XN |
Так как валовой объем продукции любой I-ой отрасли равен суммарному объему продукции, потребляемой всеми N отраслями, и конечного продукта, то должно выполняться соотношение
![]() (I = 1, 2,… N),
(I = 1, 2,… N),
Или, в сокращенной форме
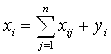 (I = 1, 2,… N). (3.1)
(I = 1, 2,… N). (3.1)
Уравнения (3.1) (их N штук) называются Соотношениями межотраслевого баланса. Единицы измерения содержащихся в уравнениях (3.1) величин могут быть натуральными и для каждого уравнения свои (кубометры, тонны, штуки и т. п.). Но они могут быть и универсальными (стоимостными). В зависимости от этого различают Натуральный И Стоимостной межотраслевые балансы. Для определенности рассмотрим далее стоимостной баланс (все величины, входящие в уравнения (3.1), выражены в рублях).
Введем Коэффициенты прямых затрат
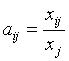 (I = 1, 2,… N), (3.2)
(I = 1, 2,… N), (3.2)
Показывающие затраты I-ой отрасли на производство единицы продукции J-ой отрасли. То есть Aij – стоимость продукции отрасли I, вложенной в 1 рубль продукции отрасли J. Так как эти коэффициенты зависят в основном от существующей технологии производства в производящих отраслях, а эта технология меняется достаточно медленно и за рассматриваемый относительно короткий период времени может считаться неизменной, то их можно считать постоянными. Это означает линейную зависимость объема Xij продукции I-ой отрасли, потребляемой J-ой отраслью, от валового объема Xj J-ой отрасли:
![]() (I = 1, 2,… N). (3.3)
(I = 1, 2,… N). (3.3)
Построенная на этом основании модель межотраслевого баланса получила название Линейной, или модели Леонтьева (американский экономист русского происхождения, лауреат Нобелевской премии по экономике).
С учетом линейных соотношений (3.3) равнения межотраслевого баланса (3.1) примут вид:
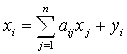 (I = 1, 2,… N). (3.4)
(I = 1, 2,… N). (3.4)
Введем обозначения:
 ;
; 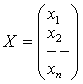 ;
; 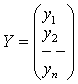 , (3.5)
, (3.5)
Где А – так называемая матрица прямых затрат, X – матрица-столбец валового выпуска, Y – матрица-столбец конечного продукта. Тогда систему (3.4) N линейных уравнений с N неизвестными (X1; X2; …Xn) можно записать в матричном виде:
![]() (3.6)
(3.6)
Система (3.6) представляет собой математическую формулировку модели Леонтьева межотраслевого баланса в матричной форме. А задача межотраслевого баланса состоит в отыскании такой матрицы-столбца валового выпуска X, который при известной матрице прямых затрат A обеспечивает заданный вектор-столбец конечного продукта Y.
В соответствии с экономическим смыслом задачи искомые элементы ![]() столбца X должны быть неотрицательны при любых неотрицательных значениях YI и AIj (I = 1, 2,… N). В таком случае модель Леонтьева называется Продуктивной.
столбца X должны быть неотрицательны при любых неотрицательных значениях YI и AIj (I = 1, 2,… N). В таком случае модель Леонтьева называется Продуктивной.
Существует несколько различных по форме Критериев продуктивности модели Леонтьева. Один из них формулируется так (доказательство опускаем): если максимум сумм элементов столбцов матрицы A прямых затрат не превосходит единицы, то есть если
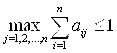 (3.7)
(3.7)
И существует номер J такой, что эта сумма строго меньше единицы
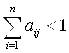 , (3.8)
, (3.8)
То модель Леонтьева (3.6) (или, что одно и то же, (3.4)) является продуктивной. Отметим, что условия (3.7) и (3.8) естественны, так как они имеют наглядный экономический смысл. Действительно,
 – (3.9)
– (3.9)
– это доля, которую составляет суммарная стоимость продукции всех отраслей, вложенная в продукцию J-ой отрасли, по отношению к общей стоимости продукции J-ой отрасли. И эта доля для любой отрасли, естественно, не должна превосходить единицу. А точнее, для рентабельной отрасли должна быть меньше единицы, ибо общая стоимость Xj продукции J-ой отрасли включает в себя и другие затраты – стоимость рабочей силы, амортизацию основных фондов и т. д., а также прибыль, получаемую отраслью от продажи продукции.
Пример 1. В таблице ниже содержатся данные баланса промышленности и сельского хозяйства в некотором регионе за некоторый период (в миллиардах рублей):
|
Отрасль |
Производственное |
Конечный |
Валовой | |
|
Промышленность |
Сельское | |||
|
Промышленность |
0,7 |
2,1 |
7,2 |
10 |
|
Сельское Хозяйство |
1,2 |
1,5 |
12,3 |
15 |
Требуется вычислить необходимый объем валового выпуска каждой отрасли, если конечный продукт промышленности увеличится вдвое, а сельского хозяйства останется на прежнем уровне.
Решение. Согласно таблицы имеем:
|
X11 = 0,7; |
X12 = 2,1; |
X21 = 1,2; |
X22 = 1,5; |
|
X1 = 10; |
X2 = 15; |
Y1 = 7,2; |
Y2 = 12,3. |
По формуле (3.2) находим коэффициенты прямых затрат:
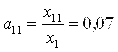 ;
;  ;
; 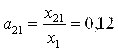 ;
; 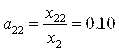
Таким образом, матрица А Прямых затрат
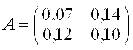
Имеет неотрицательные элементы и, очевидно, удовлетворяет критерию продуктивности, выражаемому неравенствами (3.7) и (3.8), ибо
![]() ;
; ![]() .
.
По условию задачи, в измененных условиях производства конечный продукт промышленности Y1 должен составить ![]() млрд. рублей, а конечный продукт Y2 сельского хозяйства должен остаться неизменным и составить 12,3 млрд. рублей. Поэтому для определения соответствующих валовых объемов X1 и X2 этих отраслей получаем, согласно (3.4), следующую систему линейных уравнений 2-го порядка:
млрд. рублей, а конечный продукт Y2 сельского хозяйства должен остаться неизменным и составить 12,3 млрд. рублей. Поэтому для определения соответствующих валовых объемов X1 и X2 этих отраслей получаем, согласно (3.4), следующую систему линейных уравнений 2-го порядка:
![]()
Ее главный определитель
![]()
Значит, система имеет единственное решение. Вычисляя еще два определителя неизвестных
![]()
![]()
И используя формулы Крамера (2.5), получим:
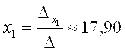 ;
; 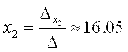 .
.
| < Предыдущая | Следующая > |
|---|