1.8. Прямая на плоскости и ее уравнение
Как известно (см. также § 5), уравнения горизонтальных, вертикальных и наклонных прямых имеют соответственно вид:
Y = B; X = A; Y = Kx + B (7.1)
Все эти уравнения – частные случаи уравнения вида
![]() , (7.2)
, (7.2)
Которое называется Общим уравнением прямой на плоскости. Общим оно называется потому, что в этом виде можно записать уравнение любой прямой на плоскости. Впрочем, для горизонтальных, вертикальных и наклонных прямых удобнее записывать их конкретные уравнения (7.1).
Остановимся подробнее на уравнениях наклонных прямых ![]() , хорошо известных еще из школьного курса математики. Прямая L с уравнением
, хорошо известных еще из школьного курса математики. Прямая L с уравнением ![]() изображена на рис. 1.22:
изображена на рис. 1.22:
|
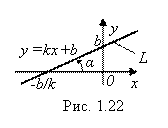
Величина ![]() называется Угловым коэффициентом прямой L (прямой
называется Угловым коэффициентом прямой L (прямой ![]() ), а величина B определяет точку пересечения этой прямой с осью Оу. Само уравнение
), а величина B определяет точку пересечения этой прямой с осью Оу. Само уравнение ![]() называется Уравнением прямой с угловым коэффициентом.
называется Уравнением прямой с угловым коэффициентом.
Для построения прямой по ее уравнению ![]() достаточно найти и нанести на плоскость Хоу любые две ее точки. Удобнее всего в качестве этих точек взять точки пересечения прямой с осями координат.
достаточно найти и нанести на плоскость Хоу любые две ее точки. Удобнее всего в качестве этих точек взять точки пересечения прямой с осями координат.
Пример 1. Построить линию L, имеющую уравнение ![]() (или, что то же самое, построить график функции
(или, что то же самое, построить график функции ![]() ).
).
Решение. Данное уравнение ![]() – это уравнение вида
– это уравнение вида ![]() при
при ![]() и
и ![]() . Но уравнение вида
. Но уравнение вида ![]() – уравнение наклонной прямой. Значит, наша линия L – наклонная прямая. Найдем точки ее пересечения с осями координат.
– уравнение наклонной прямой. Значит, наша линия L – наклонная прямая. Найдем точки ее пересечения с осями координат.
А) С осью ох: на оси Ох Y = 0, поэтому из уравнения прямой получаем: ![]() - точка пересечения прямой с осью Ох.
- точка пересечения прямой с осью Ох.
Б) С осью оу: на оси Оу X = 0, поэтому из уравнения прямой получаем: ![]() - точка пересечения прямой с осью Оу.
- точка пересечения прямой с осью Оу.
А теперь строим прямую L (рис. 1.23).
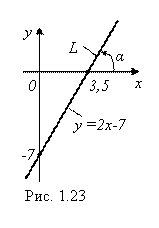 Пример 2. Найти угол
Пример 2. Найти угол ![]() , под которым прямая
, под которым прямая ![]() наклонена к оси Ох (см. рис. 1.23).
наклонена к оси Ох (см. рис. 1.23).
Решение. Из уравнения прямой ![]() определяем ее угловой коэффициент K:
определяем ее угловой коэффициент K: ![]() . Но
. Но ![]() . Значит,
. Значит, ![]() , откуда
, откуда
![]() (N = 0, ±1, ±2, …)
(N = 0, ±1, ±2, …)
Согласно таблице (таблице Брадиса) ![]() . Значит,
. Значит,
![]() (N = 0, ±1, ±2, …)
(N = 0, ±1, ±2, …)
Так как ![]() , то угол
, то угол ![]() острый (
острый (![]() ). Это подтверждает и рис. 1.23. Чтобы из предыдущей формулы получить такой угол
). Это подтверждает и рис. 1.23. Чтобы из предыдущей формулы получить такой угол ![]() , нужно в ней положить
, нужно в ней положить ![]() . В итоге получим окончательно:
. В итоге получим окончательно: ![]() .
.
А теперь рассмотрим несколько важных стандартных задач на прямые на плоскости.
Задача 1. Пусть на прямой L известна только одна ее точка M0(X0; Y0). Каким будет уравнение этой прямой?
Решение. Если эта прямая вертикальная, то ее уравнением будет, очевидно, уравнение ![]() , а если горизонтальная – то уравнение
, а если горизонтальная – то уравнение ![]() . Если же прямая L наклонная, то для полного задания этой прямой, а значит, и для возможности найти ее уравнение нужно, кроме точки M0(X0; Y0), через которую проходит прямая, задать еще и угол
. Если же прямая L наклонная, то для полного задания этой прямой, а значит, и для возможности найти ее уравнение нужно, кроме точки M0(X0; Y0), через которую проходит прямая, задать еще и угол ![]() – угол наклона прямой к оси Ох. Или, что более удобно, задать угловой коэффициент
– угол наклона прямой к оси Ох. Или, что более удобно, задать угловой коэффициент ![]() этой прямой (см. рис. 1.24).
этой прямой (см. рис. 1.24).
![]()
|
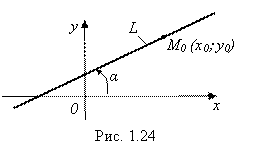
Уравнение изображенной на рис. 1.24 прямой L будем искать в виде ![]() . Величина K уже известна. А для определения величины B подставим в это уравнение координаты (X0; Y0) точки M0, лежащей на прямой. В результате найдем B:
. Величина K уже известна. А для определения величины B подставим в это уравнение координаты (X0; Y0) точки M0, лежащей на прямой. В результате найдем B:
![]()
Подставляя найденное значение B в уравнение ![]() , получим:
, получим:
![]() (7.3)
(7.3)
Это и есть искомое уравнение прямой L, изображенной на рис. 1.24 (уравнение прямой, проходящей через заданную точку M0(X0; Y0) и имеющую заданный угловой коэффициент K).
Пример 3. Найти уравнение прямой L, изображенной на рис. 1.25.
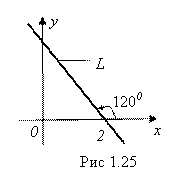 Решение. Данная прямая L проходит через точку M0(2; 0) и имеет угловой коэффициент
Решение. Данная прямая L проходит через точку M0(2; 0) и имеет угловой коэффициент
![]() .
.
Поэтому, согласно (7.3), получаем следующее уравнение прямой L:
![]()
Задача 2. Пусть теперь на наклонной прямой L заданы две какие-либо ее точки M1(X1; Y1) и M2(X2; Y2). Нужно найти уравнение этой прямой (рис. 1.26).
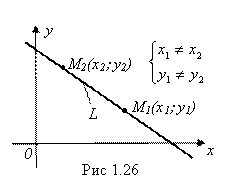 Решение. Уравнение данной наклонной прямой L будем искать в виде
Решение. Уравнение данной наклонной прямой L будем искать в виде ![]() . Здесь ни K, ни B не известны. Но зато на прямой L известны две ее точки M1(X1; Y1) и M2(X2; Y2). Подставляя координаты каждой из них в уравнение прямой
. Здесь ни K, ни B не известны. Но зато на прямой L известны две ее точки M1(X1; Y1) и M2(X2; Y2). Подставляя координаты каждой из них в уравнение прямой ![]() , получим систему двух линейных уравнений с двумя неизвестными для определения K и B. Решая ее, получим:
, получим систему двух линейных уравнений с двумя неизвестными для определения K и B. Решая ее, получим:
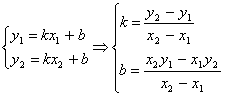 (7.4)
(7.4)
Подставляя найденные значения K и B в уравнение ![]() , после упрощений получим:
, после упрощений получим:
![]() (7.5)
(7.5)
Это и есть уравнение наклонной прямой, проходящей через две заданные точки M1(X1; Y1) и M2(X2; Y2).
Пример 4. Найти уравнение прямой, проходящей через точки А(-1; 2) и В(2; 0), и найти точку пересечения этой прямой с осью Оу.
Решение. Приняв точку А(-1; 2) за точку M1(X1; Y1), точку В(2; 0) за точку M2(X2; Y2) (а можно и наоборот!) и воспользовавшись уравнением (7.5), получим:
![]() .
.
Это и есть искомое уравнение прямой (в форме общего уравнения (7.2)). Выразив из него Y, можем записать это уравнение и в явном виде ![]() :
:
![]() .
.
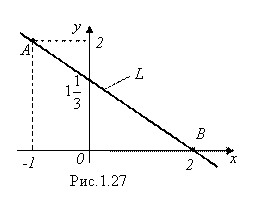
Величина ![]() и определяет точку пересечения данной прямой с осью Оу. Эта прямая L изображена на рис. 1.27.
и определяет точку пересечения данной прямой с осью Оу. Эта прямая L изображена на рис. 1.27.
Задача 3. Пусть ![]() и
и ![]() – уравнения некоторых двух данных наклонных прямых. Требуется установить:
– уравнения некоторых двух данных наклонных прямых. Требуется установить:
А) параллельны они или нет?
Б) перпендикулярны или нет?
В) если не параллельны и не перпендикулярны, то каков угол ![]() между ними?
между ними?
Решение. а) Пусть прямые L1 и L2 параллельны (рис. 1.28 (а)):
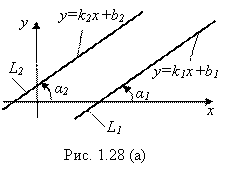
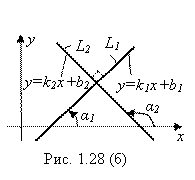
Тогда ![]() , а значит,
, а значит, ![]() , ибо
, ибо ![]() , а
, а ![]() . Обратно, если
. Обратно, если ![]() , то
, то ![]() , откуда следует, что
, откуда следует, что ![]() или что
или что ![]() отличается от
отличается от ![]() на угол
на угол ![]() (
(![]() ). В любом из этих двух случаев прямые L1 и L2 одинаково наклонены к оси Ох, а значит между собой параллельны.
). В любом из этих двух случаев прямые L1 и L2 одинаково наклонены к оси Ох, а значит между собой параллельны.
Таким образом, Прямые ![]() и
и ![]() параллельны тогда и только тогда, когда равны их угловые коэффициенты:
параллельны тогда и только тогда, когда равны их угловые коэффициенты:
![]() (7.6)
(7.6)
Условие (7.6) называется Условием параллельности прямых.
Пример 5. Показать, что прямые ![]() и
и ![]() параллельны.
параллельны.
Решение. Из уравнения первой прямой ![]() следует, что ее угловой коэффициент
следует, что ее угловой коэффициент ![]() . Чтобы получить угловой коэффициент K2 другой прямой
. Чтобы получить угловой коэффициент K2 другой прямой ![]() , нужно привести её уравнение к виду
, нужно привести её уравнение к виду ![]() - к виду с угловым коэффициентом. Делая это, получаем
- к виду с угловым коэффициентом. Делая это, получаем ![]() , откуда следует:
, откуда следует: ![]() . Так как
. Так как ![]() , то указанные прямые действительно параллельны.
, то указанные прямые действительно параллельны.
Б) Пусть прямые L1 и L2 перпендикулярны (рис. 1.28 (б)). Тогда углы их
наклона к оси Ох отличаются один от другого на прямой угол. То есть ![]() или
или ![]() . А значит, в любом случае имеет место равенство:
. А значит, в любом случае имеет место равенство: ![]() . Но тогда
. Но тогда
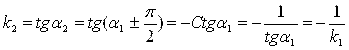
То есть получаем:
![]() (7.7)
(7.7)
Условие (7.7) является Условием перпендикулярности прямых.
Пример 6. Подтвердить перпендикулярность прямых ![]() и
и ![]() .
.
Решение. Преобразуя уравнения этих прямых к виду ![]() (к виду с угловым коэффициентом), находим:
(к виду с угловым коэффициентом), находим:
![]() ;
; ![]()
![]() ;
; ![]() .
.
Так как условие (7.7) выполняется, то указанные прямые перпендикулярны.
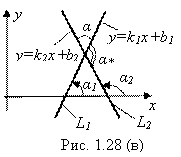
В) Пусть теперь прямые L1 и L2 составляют между собой угол ![]() (рис. 1.28 (в)), отличный от прямого. Впрочем, углом между прямыми можно, при желании, считать и угол
(рис. 1.28 (в)), отличный от прямого. Впрочем, углом между прямыми можно, при желании, считать и угол ![]() . Но так как в сумме
. Но так как в сумме ![]() и
и ![]() составляют, очевидно, 180°, то зная
составляют, очевидно, 180°, то зная ![]() , можно найти и
, можно найти и ![]() :
: ![]() .
.
Угол ![]() , согласно рис. 1.28 (в), представляет собой разность углов
, согласно рис. 1.28 (в), представляет собой разность углов ![]() и
и ![]() . То есть или
. То есть или ![]() , или
, или ![]() . Найдя
. Найдя ![]() и
и ![]() , найдем и
, найдем и ![]() .
.
Пример 7. Найти угол между прямыми ![]() и
и ![]() .
.
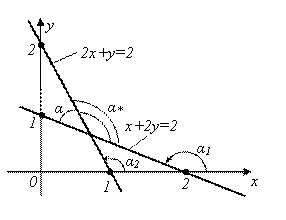 Решение. Сначала построим прямые и обозначим на рисунке интересующий нас угол
Решение. Сначала построим прямые и обозначим на рисунке интересующий нас угол ![]() .
.
Из рисунка очевидно, что ![]() . Найдем
. Найдем ![]() и
и ![]() . Для этого сначала найдем
. Для этого сначала найдем ![]() и
и ![]() – угловые коэффициенты прямых:
– угловые коэффициенты прямых:
![]() ;
; ![]()
![]() ;
; ![]() .
.
Отсюда следует:
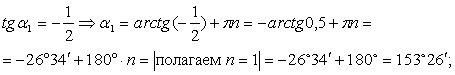
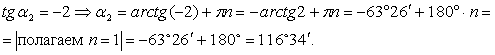
Значит,
![]() ;
; ![]() .
.
Задача 4. Пусть ![]() – уравнение некоторой прямой L на плоскости в общем виде. И пусть M0(X0; Y0) – некоторая точка плоскости, не лежащая на этой прямой. Требуется найти расстояние D от указанной точки до указанной прямой.
– уравнение некоторой прямой L на плоскости в общем виде. И пусть M0(X0; Y0) – некоторая точка плоскости, не лежащая на этой прямой. Требуется найти расстояние D от указанной точки до указанной прямой.
Решение. Рассмотрим рис. 1.29. Если данная прямая L горизонтальна или вертикальна, то решение поставленной задачи труда, естественно, не представляет. Поэтому будем считать, что L – наклонная прямая. В этом случае задачу можно решить по следующей схеме:
1. Из заданного уравнения ![]() прямой L находим ее угловой коэффициент K.
прямой L находим ее угловой коэффициент K.
2. Находим ![]() – угловой коэффициент прямой L*, проходящей через точку
– угловой коэффициент прямой L*, проходящей через точку ![]() перпендикулярно прямой L.
перпендикулярно прямой L.
3. Используя равенство (7.3), записываем уравнение прямой L*:
![]()
4. Решаем систему
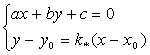
Из уравнений прямых L и L* и находим точку M1(X1; Y1) – точку их пересечения.
5. Наконец, используя формулу (3.1) для нахождения расстояния между двумя точками плоскости, находим искомое расстояние ![]() .
.
Если осуществить приведенную выше схему, то в итоге получается следующая простая формула (убедитесь в этом самостоятельно):
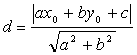 (7.8)
(7.8)
Это – формула расстояния от заданной точки ![]() до заданной прямой
до заданной прямой ![]() . Кстати, эта формула оказывается справедливой не только для наклонной, но и для горизонтальной и для вертикальной прямой (убедитесь в этом самостоятельно).
. Кстати, эта формула оказывается справедливой не только для наклонной, но и для горизонтальной и для вертикальной прямой (убедитесь в этом самостоятельно).
Пример 8. В треугольнике ABC с вершинами А(-3;0); В(2;5); С(3;2) найти длину H высоты BD.
Решение. Искомая высота H есть расстояние от точки B до прямой L, проходящей через точки A и C. Чтобы найти это расстояние, нужно сначала найти уравнение этой прямой L. Его найдем, используя уравнение (7.5) прямой, проходящей через две заданные точки:
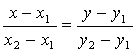 ;
; ![]() .
.
Итак, ![]() – уравнение прямой АС (в общем виде). А теперь по формуле (7.8) найдем расстояние H от точки B до этой прямой:
– уравнение прямой АС (в общем виде). А теперь по формуле (7.8) найдем расстояние H от точки B до этой прямой:
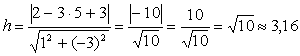 .
.
| < Предыдущая | Следующая > |
|---|