1.7. Вторая основная задача аналитической геометрии на плоскости
Эта задача обратна первой. То есть уравнение линии L дано, а по нему эту линию нужно построить. Указанная задача существенно проще первой основной задачи, и решается она стандартными методами.
Пусть, например, уравнение некоторой линии L задано в декартовых координатах в виде функции Y = F(X) (в явном виде). Требуется по данному уравнению линии L построить саму линию L. В данном случае линия L – это просто график функции Y = F(X).
В принципе, построить линию – это значит нанести на плоскость все точки линии, совокупность которых и образует линию. Точками, лежащими на линии, будут те и только те точки М (X; Y), координаты (X; Y) которых удовлетворяют уравнению линии Y = F(X). Так как на любой линии лежит бесчисленное множество точек, то определить координаты каждой из них и нанести все их на плоскость невозможно. Поэтому на практике при построении линии по ее уравнению Y = F(X) поступают так. Из области определения функции Y = F(X) (то есть из множества всех тех значений X, для которых можно найти Y) на выбранном участке оси Ох выбирают ряд значений (X1; X2; … Xn) аргумента X, и по уравнению линии Y = F(X) вычисляют соответствующий им набор значений (Y1; Y2; … Yn) функции Y. В итоге получают таблицу вида
|
Х |
Х1 |
Х2 |
… |
ХN |
(6.1) |
|
У |
У1 |
У2 |
… |
Yn |
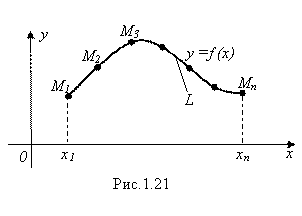 Содержащую координаты N точек (М1 (X1; Y1); М2 (X2; Y2); … МN (Xn; Yn)) искомой линии. Нанося эти точки на плоскости Xoy и соединяя их плавной кривой, строят искомую линию L (рис. 1.21). Этот хорошо известный способ называется Построением линии по точкам.
Содержащую координаты N точек (М1 (X1; Y1); М2 (X2; Y2); … МN (Xn; Yn)) искомой линии. Нанося эти точки на плоскости Xoy и соединяя их плавной кривой, строят искомую линию L (рис. 1.21). Этот хорошо известный способ называется Построением линии по точкам.
По точкам, очевидно, можно построить и линию по ее явному уравнению ![]() в полярных координатах. Для этого нужно задать ряд значений полярного угла
в полярных координатах. Для этого нужно задать ряд значений полярного угла ![]() и для них найти соответствующие значения полярного радиуса R. Затем по найденным точкам (М1 (φ1; R1); М2 (φ2; R 2); … МN (φN; R N)) строят и саму линию.
и для них найти соответствующие значения полярного радиуса R. Затем по найденным точкам (М1 (φ1; R1); М2 (φ2; R 2); … МN (φN; R N)) строят и саму линию.
Наконец, по точкам можно построить и линию, заданную уравнением в параметрической форме, то есть заданную системой уравнений вида (4.6). Для этого для ряда выбранных значений (T1; T2; … Tn) параметра T вычисляют соответствующие значения X И Y, что приводит к таблице вида:
|
T |
T1 |
T2 |
… |
Tn |
(6.2) |
|
X |
X1 |
X1 |
… |
Xn | |
|
Y |
Yn |
Yn |
… |
Yn |
В итоге находятся и точки (М1 (X1; Y1); М2 (X2; Y2); … МN (Xn; Yn)), по которым строят и саму линию.
Отметим, что качество построенной по точкам линии будет выше, если в состав точек, по которым строится линия, будут включены наиболее интересные и важные точки этой линии – ее вершины, впадины, точки пересечения линии с осями координат, точки разрыва линии, и т. д., а также будет учтена возможная симметрия линии, ее повторяемость (периодичность) и другие ее особенности. Получение всей этой важной информации о линии связано с математическим исследованием уравнения линии, на чем мы подробно остановимся позднее – в § 3 главы 4.
Примечание. Если уравнение линии задано в неявной форме (например, в виде F(х;у)=0 или в виде F(φ; R)=0), то и математическое исследование такого уравнения, и нахождение точек такой линии существенно усложняется. Например, задав в уравнении F(X;Y)=0 значение X, нам придется для нахождения соответствующего значения (значений) Y решать это уравнение относительно Y. А это может оказаться сделать и непросто. Возможно, даже придется решать это уравнение приближенно машинным путем (на ЭВМ).
Отметим еще следующее. Построение линии по ее уравнению значительно упрощается, если это уравнение принадлежит к известному типу. Например, если уравнение линии представляет собой линейную функцию вида ![]() , квадратичную функцию вида
, квадратичную функцию вида ![]() , показательную функцию вида
, показательную функцию вида ![]() , логарифмическую функцию вида
, логарифмическую функцию вида ![]() и т. д. Тогда сразу становится известен тип самой линии (прямая, парабола, показательная кривая, логарифмическая кривая и т. д.). Остается лишь установить детали этой линии. Скажем, для параболы – это направление ее ветвей, координаты вершины, точки пересечения с осями координат. После получения этой информации легко строится и сама парабола.
и т. д. Тогда сразу становится известен тип самой линии (прямая, парабола, показательная кривая, логарифмическая кривая и т. д.). Остается лишь установить детали этой линии. Скажем, для параболы – это направление ее ветвей, координаты вершины, точки пересечения с осями координат. После получения этой информации легко строится и сама парабола.
Пример 1. Построить линию, имеющую уравнение ![]() .
.
Решение. Уравнение линии представляет собой квадратичную функцию вида ![]() , где A = -1; B = 4; С = 0, поэтому данная линия – парабола. Ветви этой параболы направлены вниз, т. к.
, где A = -1; B = 4; С = 0, поэтому данная линия – парабола. Ветви этой параболы направлены вниз, т. к. ![]() . Найдем вершину параболы. Абсциссу XВ вершины найдем по известной школьной формуле:
. Найдем вершину параболы. Абсциссу XВ вершины найдем по известной школьной формуле:
![]()
А ординату вершины YВ найдем по уравнению параболы: ![]() . Итак, точка A(2;4) – вершина параболы.
. Итак, точка A(2;4) – вершина параболы.
Теперь найдем точки пересечения параболы с осью Ох. На этой оси Y=0, поэтому получаем:
![]() Þ X1 = 0 и X2 = 4.
Þ X1 = 0 и X2 = 4.
Итак, парабола пересекает ось Ох в двух точках: X1 = 0 и X2 = 4. 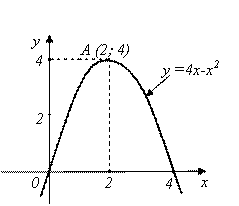 А теперь строим параболу (данных для ее построения достаточно).
А теперь строим параболу (данных для ее построения достаточно).
При построении на одном чертеже нескольких линий может возникнуть Вопрос об определении точек пересечения этих линий.
Пусть, например, Y = F1(X) и Y = F2(X) – уравнения некоторых двух линий, и требуется найти точки их пересечения. Так как искомые точки должны одновременно принадлежать обеим линиям, то и их координаты (X;Y) должны одновременно удовлетворять уравнениям обеих линий. То есть они должны удовлетворять системе
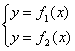 (6.3)
(6.3)
 Из уравнений этих линий. Обратно, решив систему (6.3), мы найдем такую пару (или такие пары) значений (X;Y), которые будут одновременно удовлетворять обоим уравнениям этой системы. А это значит, что точки с найденными координатами (X;Y) Лежат на обеих линиях, то есть являются точками пересечения этих линий.
Из уравнений этих линий. Обратно, решив систему (6.3), мы найдем такую пару (или такие пары) значений (X;Y), которые будут одновременно удовлетворять обоим уравнениям этой системы. А это значит, что точки с найденными координатами (X;Y) Лежат на обеих линиях, то есть являются точками пересечения этих линий.
Таким образом, Найти точки пересечения линий – это значит решить систему из уравнений этих линий.
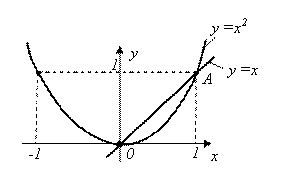
Пример 2. Найти точки пересечения прямой Y = X и параболы У=х2. Сделать иллюстрирующий чертеж.
Решение. Составим и решим систему из уравнений этих линий:
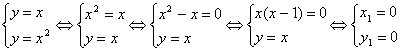 и
и 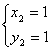 –
–
- два решения системы. Таким образом, имеются две точки пересечения данных прямой и параболы: точка O(0;0) и точка А (1;1). Иллюстрация этого представлена выше.
Упражнения
1. Построить линию, имеющую уравнение Xy = 0.
Ответ: крест из координатных осей Ох и Оу.
2. Построить линию, имеющую уравнение 2X – 3Y = 6.
Ответ: прямая, пересекающая ось Ох в точке ![]() и ось Оу в точке
и ось Оу в точке ![]() .
.
3. Найти точки пересечения прямой Y = X и кубической параболы ![]() .
.
Ответ: О(0; 0); М1(1; 1); М2(-1; -1).
4. Построить в полярных координатах линию, имеющую уравнение ![]() .
.
Ответ: кривая Архимеда. Ее удобно строить по точкам, используя таблицу значений:
|
φ |
0 |
P/2 |
P |
3p/2 |
2p |
5p/2 |
… |
|
R |
0 |
P |
2p |
3p |
4p |
5p |
… |
5. Построить линию, имеющую следующее уравнение в параметрической форме:
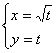
Ответ: парабола Y = X2.
| < Предыдущая | Следующая > |
|---|