1.4. Деление отрезка в заданном отношении

Рассмотрим еще одну простую, но важную задачу. Требуется найти точку М, делящую заданный отрезок М1 М2 в заданном отношении . Это значит, что искомая точка М должна занимать на отрезке М1 М2 такое положение, чтобы выполнялось условие:

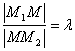( – заданное число) (3.2)

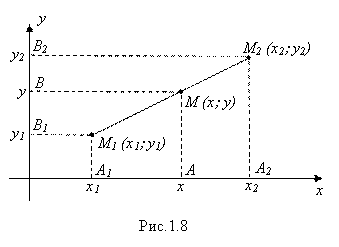Для решения поставленной задачи рассмотрим рис. 1.8.

На основании известной теоремы Фалеса о пропорциональности отрезков прямых, заключенных между параллельными прямыми, имеем:

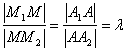
Но согласно рис. 1.8, |A1A| = X – X1, а |AA2| = X2 – X. Поэтому получаем:

Выражая отсюда X, находим:

. (3.3)

Это – абсцисса искомой точки М. Совершенно аналогично находим ее ординату Y:

(3.4)

Формулы (3.3) и (3.4) и решают поставленную задачу о делении заданного отрезка М1 М2 в заданном отношении .

В частности, если М – середина отрезка М1 М2, то = 1. Следовательно, координаты (X; Y) середины отрезка М1 М2 таковы:

; (3.5)

Примечание. Легко показать, что формулы (3.3), (3.4) и (3.5) верны не только для того расположения точек М1(X1; Y1) и М2(X2; Y2), которое указано на рис. 1.8, но и для любого другого (убедитесь в этом самостоятельно).

Пример 2. Даны точки М1(-1; 3) и М2(3; -2). На отрезке М1М2 найти точку М(X;Y), которая в два раза ближе к М1, чем к М2.

Решение. По условию задачи, искомая точка М такова, что

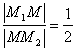
Следовательно, в данном случае рассматривается задача о делении отрезка М1 М2 в отношении . Применяя формулы (3.3) и (3.4), находим координаты точки М:

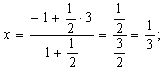
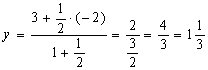
Таким образом, М = М(; ).

Упражнения

1. Точка М делит отрезок М1 М2 пополам. При этом М1 = М1(-1; -1) и М=М(0; 1). Найти координаты точки М2.

Ответ: М2 = М2(1; 3).

2. Даны две точки М1 (1; 2) и М2 (4; -1). Найти отношение , в котором делится отрезок М1 М2 точкой М своего пресечения с осью Ох, а также найти эту точку.

Ответ: = 2; М(3; 0).

< Предыдущая		Следующая >