1.3. Нахождение расстояния между точками плоскости
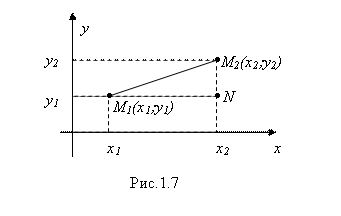 Пусть М1 (X1; Y1) и М2 (X2; Y2) – некоторые две точки плоскости в декартовой системе координат (рис. 1.7). Требуется найти формулу, по которой можно было бы находить расстояние |M1M2| между этими точками.
Пусть М1 (X1; Y1) и М2 (X2; Y2) – некоторые две точки плоскости в декартовой системе координат (рис. 1.7). Требуется найти формулу, по которой можно было бы находить расстояние |M1M2| между этими точками.
Формула эта очевидным образом вытекает из теоремы Пифагора для треугольника M1M2N. Действительно,
|M1M2|2 = |M1N|2 + |NM2|2,
Откуда ![]() . Но, согласно рис. 1.7, |M1N| = X2 – X1, а |NM2| = Y2 – Y1. Поэтому получаем окончательно:
. Но, согласно рис. 1.7, |M1N| = X2 – X1, а |NM2| = Y2 – Y1. Поэтому получаем окончательно:
![]() (3.1)
(3.1)
Это и есть та формула, по которой находят расстояние между точками плоскости в декартовой системе координат.
Примечание. Формула (3.1) выведена нами для того расположения точек М1 и М2, которое указано на рис. 1.7 (то есть когда X2 > X1 и Y2 > Y1). Но она будет верна и при любом другом расположении этих точек (подтвердите это самостоятельно).
Пример 1. Найти расстояние между точками А(0; 2) и В(4; -1).
Решение. Принимая точку А за М1, а точку В за М2 и используя формулу (3.1), получим:
![]() .
.
Естественно, тот же результат мы получим, если за точку М1 примем точку В, а за точку М2 – точку А:
![]()
| < Предыдущая | Следующая > |
|---|