1.2. Полярные координаты на плоскости
Декартовы координаты не всегда оказываются удобными. Например, для математического описания плоских фигур с круговыми границами, а также в некоторых других случаях более удобными оказываются полярные координаты.
Полярная система координат содержит лишь одну числовую ось P (Полярную ось), начало которой О называется ее Полюсом (рис. 1.4).
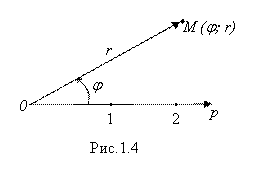
Полярными координатами произвольной точки М плоскости являются ее Полярный угол ![]() (угол между полярной осью P и направлением из полюса на эту точку), и Полярное расстояние r (расстояние от полюса O до этой точки). Полярный угол
(угол между полярной осью P и направлением из полюса на эту точку), и Полярное расстояние r (расстояние от полюса O до этой точки). Полярный угол ![]() принято считать (если нет специальной оговорки) в пределах (-P; P] и выражать в радианах. Тот факт, что
принято считать (если нет специальной оговорки) в пределах (-P; P] и выражать в радианах. Тот факт, что ![]() и R – полярные координаты точки М плоскости, обозначается так: М = М(
и R – полярные координаты точки М плоскости, обозначается так: М = М(![]() ; R).
; R).
Очевидно (см. рис. 1.4), что каждая точка М плоскости, отличная от полюса О, имеет однозначную пару полярных координат (![]() ; R). Исключение составляет лишь полюс О. У этой точки полярное расстояние R = 0, а полярный угол
; R). Исключение составляет лишь полюс О. У этой точки полярное расстояние R = 0, а полярный угол ![]() не определен. Обратно, по известным полярным координатам (
не определен. Обратно, по известным полярным координатам (![]() ; R) точки плоскости можно, очевидно, однозначно построить и саму точку.
; R) точки плоскости можно, очевидно, однозначно построить и саму точку.
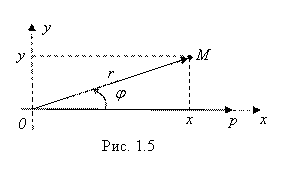
Если наряду с полярными координатами (![]() ; R) точки плоскости ввести также ее декартовы координаты, как это показано на рис. 1.5, то связь между ними выразится очевидными формулами:
; R) точки плоскости ввести также ее декартовы координаты, как это показано на рис. 1.5, то связь между ними выразится очевидными формулами:
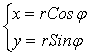 (2.1)
(2.1)
По этим формулам осуществляется переход от полярных координат точек плоскости к декартовым. Обратный переход, от декартовых координат к полярным, осуществляется по формулам,
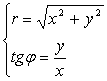 (2.2)
(2.2)
Также очевидным образом вытекающим из рис. 1.5 (или из формул (2.1)). Согласно этим формулам, полярное расстояние R точки, имеющей декартовы координаты (X; Y), находится однозначно. А полярный угол находится по предварительно вычисляемому Tg![]() . Но по Tg
. Но по Tg![]() угол
угол ![]() находится, как известно, неоднозначно:
находится, как известно, неоднозначно:
 (N = 0, ±1, ±2, …) (2.3)
(N = 0, ±1, ±2, …) (2.3)
Из множества углов ![]() , предлагаемых формулой (2.3), нужно выбрать один – тот, который соответствует четверти плоскости, в которой находится рассматриваемая точка. Это делается с помощью подбора подходящего значения целого числа N и учете того, что
, предлагаемых формулой (2.3), нужно выбрать один – тот, который соответствует четверти плоскости, в которой находится рассматриваемая точка. Это делается с помощью подбора подходящего значения целого числа N и учете того, что ![]() .
.
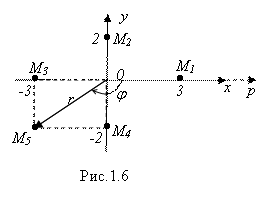 Пример 1. Найти полярные координаты изображенных на рис. 1.6 точек М1, М2, М3, М4, М5.
Пример 1. Найти полярные координаты изображенных на рис. 1.6 точек М1, М2, М3, М4, М5.
Решение. Полярные координаты (![]() ; R) точек М1, М2, М3, М4 могут быть найдены и без применения формул (2.2) и (2.3), они очевидны из рис. 1.6:
; R) точек М1, М2, М3, М4 могут быть найдены и без применения формул (2.2) и (2.3), они очевидны из рис. 1.6:
М1 (0; 3); М2 (![]() ; 2);
; 2);
М3 (![]() ; 3); М4 (
; 3); М4 (![]() ; 2).
; 2).
А вот полярные координаты (![]() ; R) точки М5 найдем, используя эти формулы:
; R) точки М5 найдем, используя эти формулы:
![]()
![]()
![]() (N = 0, ±1, ±2, …)
(N = 0, ±1, ±2, …)
Так как точка М5 находится в третьей четверти, в которой ![]() (то есть в градусах
(то есть в градусах ![]() ), то чтобы получить такой угол
), то чтобы получить такой угол ![]() для точки М5, нужно в последней формуле положить N = - 1. В итоге получим:
для точки М5, нужно в последней формуле положить N = - 1. В итоге получим: ![]() . Переведя градусы в радианы (вручную, используя тот факт, что
. Переведя градусы в радианы (вручную, используя тот факт, что ![]() =
= ![]() Рад
Рад ![]() 3,1416 рад., или, что проще, пользуясь специальной таблицей перевода градусной меры в радианную), получим:
3,1416 рад., или, что проще, пользуясь специальной таблицей перевода градусной меры в радианную), получим: ![]() -2,5534 (рад). Итак,
-2,5534 (рад). Итак,
М5 = М5(![]() ; R) = М5(-2,5534; 3,6056).
; R) = М5(-2,5534; 3,6056).
Упражнения
1. Даны точки ![]() и
и ![]() в декартовой системе координат. Найти полярные координаты этих точек.
в декартовой системе координат. Найти полярные координаты этих точек.
Ответ: ![]() ;
; ![]()
2. Даны точки ![]() и
и ![]() В полярной системе координат. Найти декартовы координаты этих точек.
В полярной системе координат. Найти декартовы координаты этих точек.
Ответ: ![]() ;
; ![]() .
.
| < Предыдущая | Следующая > |
|---|