1.1. Аналитическая геометрия на плоскости. Метод координат. Декартовы координаты

Аналитическая геометрия – это область математики, изучающая геометрические задачи средствами алгебры и математического анализа на основе метода координат.

Метод координат основан на известном из курса элементарной математики свойстве числовой оси: Каждой точке М этой оси соответствует некоторое действительно число X, и наоборот (рис. 1.1).

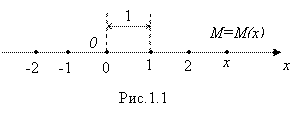Число X называется Координатой точки М, и обозначается это так: M = M(x) (читается: точка М – точка с координатой X). Координата X точки М, по определению, есть расстояние от начальной точки О (координата которой равна 0) до точки М, взятое со знаком плюс, если точка М находится справа от точки О, и со знаком минус, если она находится слева от нее.

В числовую ось, при желании, можно превратить любую прямую. Для этого следует:

А) выбрать одно из направлений этой прямой за положительное (поставить стрелку, указывающую это направление);

Б) выбрать одну из точек прямой в качестве начальной точки О (с ней связывается число 0);

В) установить на прямой масштаб измерения, то есть определиться, отрезок какой длины будет считаться единичным.

Преобразование обычной прямой в числовую ось, когда каждой точке прямой можно поставить в соответствие некоторое действительное число (координату этой точки), представляет собой введение Системы координат на прямой (рис. 1.1). После введения на прямой системы координат можно уже, очевидно, говорить не о точках этой прямой (точках М), а о соответствующих им числах X – координатах этих точек.

Далее, с помощью взаимно перпендикулярных числовых осей естественным образом устанавливается система координат на плоскости (рис. 1.2) и система координат в пространстве (рис. 1.3). Рисунок 1.2 демонстрирует, что у каждой точки M = M (X; Y) плоскости имеются две координаты: абсцисса X (проекция точки М на числовую ось Ox) и ордината Y (проекция точки М на числовую ось Oy). Аналогично рис. 1.3 демонстрирует три координаты точки M = M (X; Y; Z) в пространстве: абсциссу X, ординату У и аппликату Z, являющиеся проекциями этой точки на числовые оси Y Ox, Oy и Oz Соответственно.

Указанные координаты точек на плоскости и в пространстве называются Прямоугольными или декартовыми – в честь Рене Декарта, который ввел в обиход математики эти координаты.

Опираясь на приведенное выше понятие координат точек прямой, плоскости и пространства (рис. 1.1 – 1.3), можно теперь Любое действительное число X считать точкой числовой оси Ox (точкой одномерного пространства); любую пару чисел (x; y) – точкой плоскости Xoy (точкой двумерного пространства); любую тройку чисел (x; y; z) – точкой обычного пространства (трехмерного). И вообще, любую упорядоченную совокупность N действительных чисел (X1; X2; … Xn) можно считать Точкой некоего n-мерного пространства. Для N > 3 такое пространство является математической абстракцией (физически непредставимо). И тем не менее введение в математику таких пространств оказалось очень плодотворным и для дальнейшего развития самой математики, и для ее приложений в других науках.

Обратно, после введения системы координат на прямой, плоскости и в пространстве Каждую точку прямой можно считать просто числом; каждую точку плоскости – парой чисел; каждую точку пространства – тройкой чисел. Эти числа – координаты соответствующих точек. Таким образом, появляется возможность взамен точек (геометрических объектов) рассматривать Числа (алгебраические объекты). Эта замечательная возможность позволяет также (мы увидим это позже) вместо линий, поверхностей, плоских фигур и пространственных тел, то есть вместо Геометрических объектов рассматривать некие функции, уравнения, неравенства и т. д., то есть Алгебраические объекты. Таким образом, появляется возможность преобразовывать геометрические задачи в задачи алгебры и математического анализа, которые обычно решаются проще. В этом, в принципе, и состоит идея метода координат.

Примечание. Упорядоченную совокупность произвольных N чисел можно считать не только точкой, но и Вектором n-мерного пространства. Такое представление тоже оказалось очень плодотворным и для самой математики, и для ее приложений, в том числе приложений в экономике. Но углубляться в это в нашем курсе не будем.

Следующая >