1.5. Линии на плоскости и их уравнения

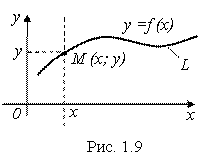
Пусть на плоскости с декартовой системой координат изображена некоторая линия L (рис. 1.9). И пусть это такая линия, что каждая вертикальная прямая, пересекающая линию, пересекает ее только один раз (как на рис. 1.9). Тогда, зная абсциссу Х любой точки М (X; Y) этой линии, можно однозначно найти её ординату У. Таким образом, указанная линия L устанавливает однозначное соответствие между двумя переменными Х и У (координатами её точек), а значит, Определяет некоторую функцию

(4.1)

Сама же линия L является Графиком этой функции.

Функция (4.1) является, по своей сути, некоторым уравнением. Ему удовлетворяют координаты (Х; У) любой точки линии L и только они. Вот такое уравнение, по определению, и называется Уравнением линии. Естественно, что у разных линий будут и разные уравнения. Уравнение линии указывается рядом с линией (см. рис. 1.9).

Мы предполагали, что вертикальные прямые, пересекающие линию L, пересекают ее только один раз. Если это не так, но зато таким свойством обладают горизонтальные прямые, то тогда по ординатам Y точек линии будут однозначно определяться их абсциссы X. И тогда уравнение линии можно будет записать в виде функции

X = G(Y) (4.2)

(здесь использована другая буква для обозначения функции, ибо функции (4.1) и (4.2) – разные даже для одной и той же линии).

А теперь будем считать, что L – совершенно произвольная (например, замкнутая) линия, которую некоторые (или даже все) и вертикальные, и горизонтальные прямые пересекают более, чем один раз. У такой линии уже не может быть уравнения ни в форме (4.1), ни в форме (4.2). Но такие уравнения (в той или другой форме) будут у отдельных кусков линии. Далее, может оказаться, что уравнения различных кусков линии можно объединить в некотором едином уравнении вида

F(X; Y) = 0 (4.3)

И этому уравнению удовлетворяют координаты (X; Y) Любой точки линии, и только они. Тогда уравнение (4.3) будет являться уравнением данной линии. Такое уравнение называется Неявным уравнением линии, ибо в нем ни одна из переменных не выражена через другую – в отличие от Явных уравнений (4.1) и (4.2).

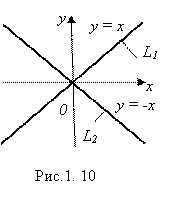Пример 1. Рассмотрим рис. 1.10, на котором изображена прямая L1 – биссектриса первого и третьего координатных углов, и прямая L2 – биссектриса второго и четвертого координатных углов. Уравнения этих прямых очевидны: – уравнение L1, – уравнение L2. Это – Явные уравнения типа (4.1). Их можно записать и в явном виде типа (4.2): и . А теперь рассмотрим объединение этих прямых, то есть линию L, представляющую собой крест из прямых L1 и L2. Чтобы записать уравнение этого креста, нужно объединить в одно уравнение уравнения и прямых, образующих этот крест. И это уравнение очевидно: . Действительно, выражая из него Y, получим две функции и , то есть получим уравнения тех двух прямых, которые образуют крест. Кстати, полученное уравнение креста – уравнение типа (4.3), то есть неявное уравнение.

Из различных форм уравнения линии наиболее удобной является форма (4.1), потому что в этом случае уравнение линии представляет собой обычную функцию . А значит, исследование уравнения линии означает исследование функции, что является классической и хорошо разработанной математической процедурой. В принципе так же удобно иметь дело и с уравнением линии в форме (4.2). А вот неявное уравнение линии в форме (4.3) гораздо менее удобно для исследования. Поэтому такое уравнение стараются перевести (преобразовать) в явную форму (4.1) или (4.2), выражая из него Y через X или X через Y (если это возможно). Если это не удается, приходится иметь дело с неявным уравнением (4.3), которое труднее, но тоже поддается математическому исследованию.

Пример 2. Пусть – неявное уравнение некоторой линии. Выразив из него Y, получим . Это уже явное уравнение той же линии, и теперь даже ясно, какой – параболы.

Примечание. Перенеся в уравнениях (4.1) и (4.2) правую часть налево, мы сделаем эти явные уравнения неявными. Поэтому неявное уравнение линии в форме (4.3) является наиболее общим – в этом виде можно записать уравнение любой линии на плоскости с декартовой системой координат. Но не всякое такое уравнение является уравнением какой-то линии на плоскости. Например, уравнение удовлетворяется, очевидно, лишь при X = 0 и Y = 0 одновременно и, следовательно, определяет лишь одну точку плоскости – точку O(0;0). А уравнение не может быть удовлетворено ни при каких X и Y, а значит, вообще никаких геометрических объектов на плоскости не определяет. Но такие случаи малосодержательны, являются исключениями, поэтому на них останавливаться и смысла нет.

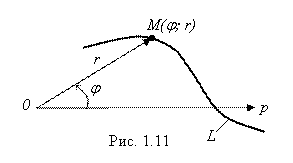Если на плоскости вместо декартовой системы координат введена полярная система, и на этой плоскости содержится некоторая линия L (рис. 1.11), то уравнение этой линии будет связывать уже не декартовы координаты (X; Y) произвольной точки М линии L, а ее полярные координаты (; R). При этом если каждому будет соответствовать вполне определенное R, то линия L задает R как функцию от :

(4.4)

Эта функция будет явным уравнением линии L В полярных координатах. В противном случае уравнением линии L в полярных координатах будет некое неявное уравнение вида

(4.5)

Наконец, уравнение линии на плоскости иногда записывают и в так называемой Параметрической форме.

Пусть, например, по плоскости с введенной на ней декартовой системой координат движется точка М, положение которой в каждый момент времени T известно. Это значит, что координаты (X; Y) движущейся точки заданы как некие функции времени:

(4.6)

Система (4.5) определяет движение указанной точки М(X; Y) по плоскости, а значит, определяет и траекторию L движущейся точки. Эта система называется Параметрическим уравнением линии L на плоскости. В нем координаты (X; Y) точек линии связаны не непосредственно друг с другом (как в формах (4.1) – (4.3)), а через посредника – параметр T. Исключив из системы (4.6) этот параметр, мы можем связать X и Y непосредственно друг с другом. Кстати, параметр T в системе (4.6) может иметь и какой-то другой смысл, не обязательно представлять собой время.

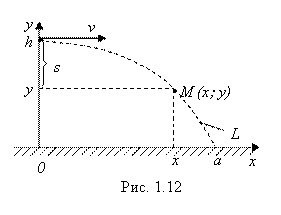
Пример 3. Материальная точка поднята над поверхностью земли на высоту H и брошена горизонтально со скоростью V. Найти уравнение траектории L брошенной точки. Сопротивлением воздуха пренебречь.

Решение. Рассмотрим рис. 1.12. Так как брошенная точка участвует одновременно в двух независимых движениях – равномерном горизонтально со скоростью V и равноускоренном вертикально с ускорением свободного падения G, то в любой момент времени координаты (X; Y) движущейся точки М найдутся по хорошо известным из школьной физики формулам:

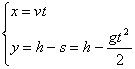() (4.7)

Это и есть уравнение траектории L брошенной точки (параметрическое). Его, при желании, можно привести и к явному виду (4.1). Для этого из первого уравнения системы (4.7) выразим параметр и подставим его во второе уравнение. В итоге получим явное уравнение траектории L (параболы):

. (4.8)

Кстати, положив в (4.8) Y = 0 и X = A, найдем дальность полета A:

. (4.9)

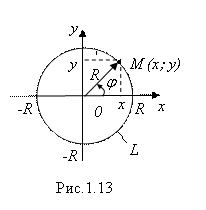Пример 4. Рассмотрим окружность радиуса R с центром в начале декартовой системы координат (рис. 1.13). Из рисунка очевидно, что для каждой точки М(X; Y) указанной окружности L выполняются равенства:

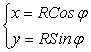(], (4.10)

Где – полярный угол точки М. Система (4.10) имеет вид (4.6) при и, следовательно, представляет собой параметрическое уравнение окружности L (параметром является угол ).

Можно связать X и Y и напрямую друг с другом, без посредника . Для этого возведем каждое уравнение (4.10) в квадрат и сложим их. В итоге получим:

(4.11)

Это – уравнение окружности L в декартовых координатах в неявной форме (в форме (4.3)). Выражая из этого уравнения Y, можем привести его и к явной форме (форме (4.1)):

(4.12)

Равенство (4.12) содержит два уравнения. При этом – это явное уравнение верхней полуокружности, а – нижней.

Упражнения

1. Решить задачу, рассмотренную в примере 3, когда точка брошена не горизонтально, а под некоторым углом к поверхности земли.

Ответ: 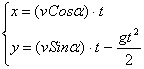– в параметрической форме (t ³ 0 – время).

2. Точка движется в полярной системе координат по кривой Архимеда, если ее движение представляет собой наложение (суперпозицию) двух независимых движений: равномерного радиального движения с некоторой линейной скоростью V и равномерного вращения радиальной прямой вокруг полюса с некоторой угловой скоростью . Найти уравнение кривой Архимеда, если в начальный момент времени точка двинулась вдоль полярной оси.

Ответ: .

< Предыдущая		Следующая >