Перечень умений
|
№ п/п |
Умение |
Алгоритм |
|
1 |
Точка на плоскости А) Определить, лежит ли точка |
1. В уравнение плоскости подставить вместо текущих координат x, y, z координаты данной точки
2. Если при этом получится тождество (верное равен-ство), то точка |
|
Б) Найти координаты какой-нибудь точки |
1. Двум координатам из трех следует присвоить произвольные значения: причем, если 2. Подставить выбранную пару координат в уравнение плоскости. 3. Из полученного относительно третьей координаты уравнения, найти значение этой координаты | |
|
2 |
Найти вектор |
1. Проверить, будут ли векторы 2. Найти векторное произведение
3. Положить вектор |
|
3 |
Найти расстояние d от точки |
Вычислить расстояние d по формуле
|
|
4 |
Каноническое и параметрическое уравнение прямой А) Написать каноническое уравне-ние прямой по двум точкам |
1. Вычислить координаты вектора
2. Взять направляющим вектором прямой 3. Написать каноническое уравнение прямой, прохо-дящей через точку
|
|
Б) Написать параметрическое урав-нение прямой, заданной канони-ческим уравнением |
1. Обозначить коэффициент пропорциональности через t (параметр) 2. Из полученных равенств выразить координаты |
|
№ п/п |
Умение |
Алгоритм |
|
5 |
Написать каноническое уравнение прямой, заданной как пересечение двух плоскостей
( |
1. Найти какую-нибудь точку Одной из переменных следует присвоить произвольное значение (удобно брать значение равное нулю) и решить систему из двух уравнений с двумя неизвестными: если 2. Выписать координаты векторов нормали 3. Найти векторное произведение 4. Взять направляющим вектор прямой
5. Написать каноническое уравнение прямой
|
|
6 |
Найти точку |
1. Записать параметрические уравнения заданной прямой (см. ум. 4). 2. Полученные выражения для координат
3. Из последнего уравнения вычислить значение параметра T. 4. а) если найденное значение T единственно, то под-ставив его в параметрическое уравнение прямой, получим единственную точку пересечения Б) если уравнение для T несовместно, точек Пересе-чения нет, прямая параллельна плоскости; В) если уравнение справедливо при любом T , то прямая лежит на плоскости – точек пересечения множества. Замечание. Фактически здесь описан один из способов решения совместного уравнения плоскости и прямой |
|
№ п/п |
Умение |
Алгоритм |
|
7 |
Определить тип поверхности второго порядка и ее основные параметры по общему уравнению (в уравнении отсутствуют произве-дения координат)
|
1. В выражениях 2. Выписать преобразование координат при параллельном сдвиге системы координат в «новое» начало 3. Подставить полученные выражения в уравнение записанное в п.1, получить каноническое уравнение поверхности. 4. По каноническому уравнению определить тип поверхности и ее параметры. |
|
8 |
Определить по каноническому уравнению цилиндра второго порядка: а) уравнение его направ-ляющей; б) какой из координатных осей параллельны его образующие. |
1. Уравнение направляющей (в одной из координат-ных плоскостей) совпадает с уравнением цилиндра. 2. Образующие параллельны той координатной оси, «название» которой в уравнении цилиндра отсутствует (например, если отсутствует Z – то оси OZ). 3. Построить чертеж |
| < Предыдущая | Следующая > |
|---|
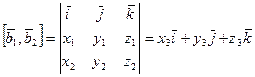 .
.

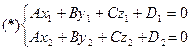
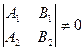 , то положить
, то положить  , то -
, то - 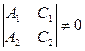 , то -
, то -  выделить полные квадраты и записать исходное уравнение в виде:
выделить полные квадраты и записать исходное уравнение в виде: 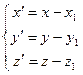 .
.